Can we strengthen the extension theorem for zero trace functions?

Question

I am reading Evans PDE book and I am working up to the Sobolev Embedding Theorem. While reading through the proof of the fact that all $u\in W^{1,p}(U)$ that satisfy $Tu=0$ are also in $W^{1,p}_0(U)$. However, the setup feels a bit loose. From page 274,

Using partitions of unity and flattening out $\partial U$ as usual, we may as well assume $$\begin{cases}u\in W^{1,p}(\Bbb R^n_+),& u~\text{has compact support in}~\bar{\Bbb R}^n_+, \\ Tu=0~\text{on}~\partial\Bbb R^n_+\end{cases}$$

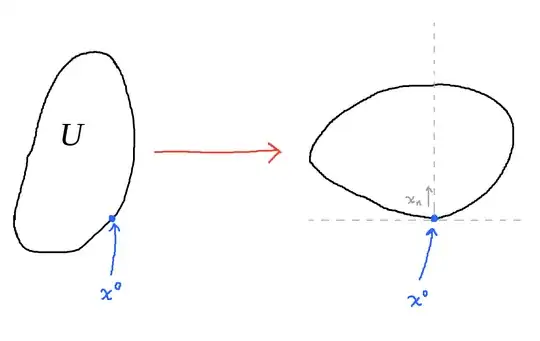
Basically what Evans is doing here is choosing some point $x^0\in\partial U$ and making a change of coordinate such that $x_0$ is the new origin and the $x_n$ axis is exactly aligned with the negative of the outward normal vector to $\partial U$ at $x^0$, like below:

I don't see how we can guarantee that $u=0$ in $\Bbb R^n\setminus \bar{\Bbb R}^n_+$. In the statement of the extension theorem, we could only guarantee that $ \operatorname{supp}(Eu)=V$ for some $V\supset\supset U$. In other words, when extending functions $u\in W^{1,p}(U)$ to $W^{1,p}(\Bbb R^n)$, we in general need to have a little bit of "wiggle room" to damp down the values of $u$ and $D^\alpha u$ before we can safely set it to zero everywhere else, in order to maintain integrability of $D^\alpha u$. This to me makes sense.

However, Evans appears to be asserting, without proof, that in the special case where $Tu=0$, that no wiggle room is required. With the statement of the Extension theorem below:

THEOREM (Extension Theorem). Assume $U\subset \Bbb R^n$ is open and bounded, with $C^1$ boundary. Choose any open set $V\subseteq \Bbb R^n$ such that $U\subset \subset V$. Then, there exists a bounded linear operator $$E:W^{1,p}(U)\to W^{1,p}(\Bbb R^n)$$ such that for all $u\in W^{1,p}(U)$,

(i) $Eu=u$ almost everywhere in $U$,

(ii) $\operatorname{supp}(Eu)\subseteq V$ and

$$\Vert Eu\Vert_{W^{1,p}(\Bbb R^n)}\leq C \Vert u\Vert_{W^{1,p}(U)}$$ For some $C\geq 0$ depending only on $p$, $U$, and $V$.

Evans appears to be asserting the additional statement:

$$\text{Additionally, if}~~Tu=0, ~\text{then}~\operatorname{supp}(Eu)\subseteq U.\tag{☆}$$

---

My questions: Is $(☆)$ true? In other words, for functions $u\in\ker T$, is the trivial extension $$E u=\begin{cases}u & \text{in}~U \\ 0 & \text{in}~\Bbb R^n\setminus U\end{cases}$$ Also a valid extension, in the sense that $Eu\in W^{1,p}(\Bbb R^n)$ and that it obeys (ii) ? Essentially this boils down to showing that for zero-trace functions, there cannot be any bad discontinuities on $\partial U$. To me this seems intuitively obvious, but I can't quite pin down the details.

I would be happy if someone could provide a proof of this even by first taking for granted that $\ker T=W^{1,p}_0$, even though this is the thing I am trying to prove in the first place. This is purely a matter of intellectual curiosity at this point.

More directly, is there any way that I can understand Evans's construction, without needing an improvement of the Extension theorem first? In particular, how can I see that the aforementioned "wiggle room" is not needed?

Answer 1

There are two different extension theorems at play.

(1) the first one is the general Sobolev extension theorem. In my version of Evans' book it is contained in section 5.4 (titled ``Extensions''). There, an extension operator $E : W^{1,p}(U) \to W^{1,p}(\mathbb R^d)$ is constructed by reflection. From the construction, it follows that $E$ is linear and continuous from $W^{1,p}(U)$ to $W^{1,p}_0(V)$ and to $W^{1,p}(\mathbb R^d)$.

This extension $Eu$ is not zero outside of $U$ even if the function $u\in W^{1,p}(U)$ has zero trace. See the construction of $\bar u$ in the first part of the proof, where the extension from a half-ball to a full ball is constructed.

I.e., the extension of $u(x) = \sin( x)$ from $(0,2\pi)$ is given by $\bar u(x) = -3 \sin(-x) + 4\sin(-x/2)$ for negative $x$ (not by $\bar u(x)=0$).

Hence, the claim (☆) is not true.

(2) the second one concerns $W^{1,p}_0(U)$ functions. In section 5.5 (``traces''), after proving the trace theorem, it is proven that if $u \in W^{1,p}(U)$ with zero trace ($Tu=0$) then $u\in W^{1,p}_0(U)$. In the proof, no extension is done. This implies that the operator $Z$ defined by $$ Zu = \begin{cases} u & \text{ in } U,\\ 0 & \text{ in } U^c,\\ \end{cases} $$ is linear and continuous as map into $W^{1,p}_0(\mathbb R^d)$.

To see this implication take $u \in W^{1,p}(U)$ with $Tu=0$. Then that result implies $u \in W^{1,p}_0(U)$. Hence, there is a sequence $u_k$ with $u_k \in C_c^\infty(U)$ with $u_k \to u$ in $W^{1,p}(U)$. Due to compact support, $Zu_k \in C_c^\infty(\mathbb R^d)$. Trivially $Zu_k \to Zu$ on $W^{1,p}( (\bar U)^c)$ as everything is zero on $(\bar U)^c$. Since the boundary of $U$ has zero measure, it follows $Zu_k \to Zu$ on $W^{1,p}(\mathbb R^d)$, so that $Zu \in W^{1,p}(\mathbb R^d)$.

Note that $Z \ne E$.

This should also answer the question/confusion

I don't see how we can guarantee that $u=0$ in $\Bbb R^n\setminus \bar{\Bbb R}^n_+$.

At that point of the proof $u$ is smooth with compact support in $\mathbb R_n^+$. Hence, its extension by zero is smooth (trivially?). Note that this proof does not invoke the earlier extension theorem about the existence of $E$.

Answer 2

This is solved by one small observation. In the setup, I missed the bar over $\mathbb R$. I.e, the statement

$$u~\text{has compact support in}~\overline{\mathbb R^n_+}$$

Does not imply $u=0$ on $\partial \mathbb R^n_+$. It simply implies $u=0$ in $\Bbb R^n\setminus \mathbb R^n_+$.

Answer 3

As far as I can tell, Evans does implicitly assume the admissibility of the zero extension, without providing formal justification. The purpose of this answer is to provide the justification that I was looking for.

---

---

---

THEOREM: (Admissibility of the zero extension for zero trace functions.)

Let $n\in\mathbb N$ and let $U\subset\mathbb R^n$ be an open, bounded set with $C^1$ boundary. Let $p\in [1,\infty)$ and suppose $u\in W^{1,p}(U)$. We define the zero extension operator $Z$ as $$Zu:=\begin{cases} u & \text{in}~U \\ 0 & \text{in}~\Bbb R^n\setminus U \end{cases}$$ Note: $Zu$ is also sometimes called the trivial extension of $u$. Then, for all $u\in \ker T$ where $T$ is the trace operator, then $Zu$ is a valid extension of $u$ from $U$ to $\mathbb R^n$, in the sense that it obeys all of the properties of the classical (reflection-based) extension $E$, i.e

$(\mathrm i)$ $Zu=u$ a.e in $U$,

$(\mathrm{ii})$ $Zu\in W^{1,p}(\mathbb R^n)$,

$(\mathrm{iii})$ $Zu$ is compactly supported in $\mathbb R^n$,

$(\mathrm{iiii})$ $\exists C>0$, not depending on $u$, such that $\Vert Zu \Vert_{W^{1,p}(\mathbb R^n)}\leq C\Vert u \Vert_{W^{1,p}(U)}$.

PROOF: Items (i), (iii), and (iiii) all follow directly from the definition of the zero extension, as long as (ii) holds. (i.e take $C=1$ and clearly also $\operatorname{supp}(Zu)\subseteq \bar U$) Therefore we need only show (ii), in other words, we need only show that $Zu$ has weak derivatives. For this we need the following Lemma:

---

Lemma: (Integration by parts in Sobolev spaces on bounded domains with $C^1$ boundary.) Define $n,U,p,u$ as in the above theorem and once again assume $U$ has a $C^1$ boundary. Again denote by $T$ the trace operator $T:W^{1,p}(U)\to L^p(\partial U)$. Then, for any function $\phi\in C^\infty (\bar U)$, we have the following integration by parts formula: $$\int_U uD\phi~\mathrm d\mu^n=-\int_U \phi Du~\mathrm d\mu^n+\int_{\partial U}(Tu)\phi\nu~\mathrm d\mu^{n-1}\tag{1}$$ Where $\nu$ is the unit outward normal to $\partial U$. Proof: Owing to the well-behaved boundary of $U$, we can find functions $(u_m)_{m\in\mathbb N}\in C^\infty(\bar U)$ such that $u_m \overset{m\to\infty}{\longrightarrow}u$ in $W^{1,p}(U)$, and, $u_m\overset{m\to\infty}{\longrightarrow} Tu$ on $L^p(\partial U)$. First, it is clear, as a simple consequence of the divergence theorem that for any $v\in C^\infty (\bar U)$, our integration by parts formula holds where the boundary values of $v$ exist classically, i.e $$\int_U vD\phi~\mathrm d\mu^n=-\int_U \phi Dv~\mathrm d\mu^n+\int_{\partial U}(v|_{\partial U})\phi\nu~\mathrm d\mu^{n-1}$$

Therefore, as $u_m\in C^\infty(\bar U)$ for all $m$, the sequence $$a_m:=\int_U D(\phi u_m)~\mathrm d\mu^n-\int_{\partial U} (u_m|_{\partial U})\phi\nu~\mathrm d\mu^{n-1}$$ Satisfies $a_m=0$ for all $m$, and hence $(a_m)_{m\in\Bbb N}$ is convergent with limit $0$. Because we can interchange integrals and limits in $L^p$, the limit may be computed also as $$0=\lim_{m\to\infty}a_m=\int_U D\left(\phi \lim_{m\to\infty}u_m\right)~\mathrm d\mu^n-\int_{\partial U} \left(\lim_{m\to\infty}u_m|_{\partial U}\right)\phi\nu~\mathrm d\mu^{n-1} \\ =\int_U D(\phi u)~\mathrm d\mu^n-\int_{\partial U}(Tu)\phi\nu~\mathrm d\mu^{n-1}$$ Expanding the product rule and rearranging gives the desired formula $(1)$.

---

Armed with this knowledge, we show that $Zu$ has a weak derivative in all of $\Bbb R^n$. Letting now $\phi\in C^{\infty}_{\text{comp}}(\mathbb R^n)$ be smooth and compactly supported we can easily see $$\int_{\Bbb R^n}(Zu)D\phi~\mathrm d\mu^n=\int_{U}(Zu)D\phi~\mathrm d\mu^n=\int_{U}uD\phi~\mathrm d\mu^n \\ =-\int_U \phi Du~\mathrm d\mu^n+\int_{\partial U}\underbrace{(Tu)}_{=0}\phi\nu~\mathrm d\mu^{n-1} \\= -\int_U \phi D(Zu)~\mathrm d\mu^{n} \\ =-\int_{\Bbb R^n}\phi D(Zu)~\mathrm d\mu^n$$ Thus $Zu$ has a weak derivative in $\Bbb R^n$.

Remark: Though the trivial extension shares the same properties as the reflection extension for functions in $\ker T$, the trivial and reflection extensions are not identically equal. Additionally, whereas the reflection extension also preserves the existence of the weak second derivatives for functions $u\in W^{2,p}(U)$, the zero extension does not. For instance, consider $n=1,U=(-1,1)$. Then the function $u:(-1,1)\to\mathbb R$ defined by $$u(x)=\sqrt{2-x^2}-1$$ Is in $W^{2,p}(U)\cap \ker T$, however, $Zu\notin W^{2,p}(\Bbb R)$, as $Zu$ has no weak second derivative in $\Bbb R$.