How to maximize the product of areas in a disk?

Question

A disk is divided into $n$ regions by drawing $n$ evenly spaced points on the perimeter and then drawing line segments joining one fixed point with all the other points.

Here is an example with $n=6$.

For a given large radius $R$, what value of $n$ will maximize the product of the areas of the regions, in terms of $R$?

Numerical investigation suggests that the product of the areas is maximized when $n\approx\dfrac{\pi R^2}{2e}$.

(If, instead, the disk (or any shape) is divided into $n$ regions of equal area, then the product of areas is maximized when $n\approx\dfrac{\pi R^2}{e}$. Proof.)

My attempt

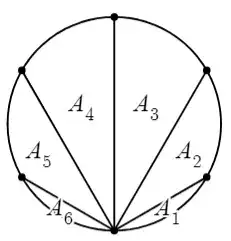
Let $A_1,A_2,\dots,A_n$ be the areas of the regions, as shown.

Using the formula for the area of a segment, we have

$$A_1+A_2+\cdots+A_k=\frac12R^2\left(\frac{2k\pi}{n}-\sin\left(\frac{2k\pi}{n}\right)\right)$$

Thus,

$$A_k=\frac12R^2\left(\frac{2k\pi}{n}-\sin\left(\frac{2k\pi}{n}\right)\right)-\frac12R^2\left(\frac{2(k-1)\pi}{n}-\sin\left(\frac{2(k-1)\pi}{n}\right)\right)$$

Simplifying, and using a sum to product identity, we have

$$A_k=R^2\left(\frac{\pi}{n}-\sin\left(\frac{\pi}{n}\right)\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$

So the product of the areas is

$$P(n)=R^{2n}\prod_{k=1}^{n}\left(\frac{\pi}{n}-\sin\left(\frac{\pi}{n}\right)\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$

I don't know what to do with this.

Context

This question was inspired by "Product of areas in a disk".

Answer 1

$$S_n=\sum_{k=1}^n\log\left(1-\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$ Since we know the antiderivative, using Euler-Maclaurin summation to any order $$S_n=-n \log(2)+C$$ and then your result.

If we just replace the summation by the integral $$T_n=\int_{1}^n\log\left(1-\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$ $$T_n=-n \log (2)+2 \log (n)+\log \left(\frac{2 e^2}{\pi ^2}\right)+\frac{\pi ^2}{36 n^2}+O\left(\frac{1}{n^4}\right)$$ and the approximate minimum is $$n_*=\frac{2}{W\left(\frac{4 e}{\pi R^2}\right)}$$ which is asymptotic to your number.

Answer 2

(Self-answering)

Start with OP's expression for the product of areas.

$$P(n)=R^{2n}\prod_{k=1}^{n}\left(\frac{\pi}{n}-\sin\left(\frac{\pi}{n}\right)\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$

Take the log of both sides.

$$\ln P(n)=n\ln R^2+\sum_{k=1}^n\ln\left(\frac{\pi}{n}-\sin\left(\frac{\pi}{n}\right)\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$

For large $n$, we can approximate $\sin\left(\frac{\pi}{n}\right)\approx\frac{\pi}{n}$

$$\ln P(n)\approx n\ln R^2+n\ln\left(\frac{\pi}{n}\right)+\sum_{k=1}^n\ln\left(1-\cos\left(\left(\frac{2k-1}{n}\right)\pi\right)\right)$$

For large $n$, the series can be approximated by $n\int_0^1\ln\left(1-\cos(2\pi x)\right)dx$ which equals $-n\ln 2$ (the proof is shown below).

$$\ln P(n)\approx n\ln R^2+n\ln\left(\frac{\pi}{n}\right)-n\ln 2$$

Switch from discrete $n$ to continuous $x$, and combine logs.

$$\ln P(x)=x\ln\left(\frac{\pi R^2}{2x}\right)$$

Differentiate implicitly with respect to $x$ and set $P'(x)=0$.

$$x\left(\frac{2x}{\pi R^2}\right)\left(-\frac{\pi R^2}{2x^2}\right)+\ln\left(\frac{\pi R^2}{2x}\right)=0$$

$$x=\frac{\pi R^2}{2e}$$

Thus, the product of areas is maximized when $n\approx \dfrac{\pi R^2}{2e}$.

(Fun fact: It follows that, when the product of areas is maximized, the log of the product is approximately equal to $n$.)

---

Proof that $\int_0^1\ln\left(1-\cos(2\pi x)\right)dx=-\ln 2$

$\begin{align} I & = \int_0^1\ln\left(1-\cos(2\pi x)\right)dx \\ & \overset{x\to x/\pi}{=}\frac{1}{\pi}\int_0^\pi\ln(1-\cos (2x))dx \\ & = \frac{1}{\pi}\int_0^\pi\ln(2\sin^2x)dx \\ & = \ln2+\frac{2}{\pi}\int_0^\pi\ln(\sin x)dx\\ & = \ln2+\frac{4}{\pi}\int_0^{\pi/2}\ln(\sin x)dx\\ \end{align}$

We have $\int_0^{\pi/2}\ln(\sin x)dx=-\frac{\pi}{2}\ln 2$.

$\therefore I=-\ln 2$