Is the function $f(x) = \sum_{k=1}^\infty (-1)^{k+1} \sin(x/k)$ bounded on $\mathbb{R}$?

Question

Consider the function $f: \mathbb{R} \to \mathbb{R}$ defined by the series:

$$f(x) = \sum_{k=1}^\infty (-1)^{k+1} \sin(x/k)$$

For any fixed $x \in \mathbb{R}$, the series converges by the Alternating Series Test, so the function $f(x)$ is well-defined everywhere.

Is this function $f(x)$ bounded on $\mathbb{R}$? Using the following plot, it clearly seems that this isn't the case. This has already been explored a bit here, but my focus is on proving that this is unbounded.

I have been looking at this question for several years and tried a lot of transformations to the function (Mellin, Taylor series, ...), looked at Entire Function theory but none of the representations readily yielded a proof.

My current best strategy assumes $f(x)$ is bounded (for contradiction). This assumption implies a finite average squared value, $\|f\|^2 = \limsup_{T\to\infty} \langle f, f \rangle_T < \infty$, derived from the time-averaging inner product $\langle g, h \rangle_T = \frac{1}{T}\int_{0}^T g(x)h(x)dx$. Using the orthogonal span $\psi_k(x)=\sin(x/k)$ and calculate the generalized coefficients $c_k = \lim_{T\to\infty} \langle f, \psi_k \rangle_T = (-1)^{k+1}/2$. The divergence $\sum |c_k|^2 = \infty$ suggests a contradiction via Bessel inequality : $\sum |c_k|^2 \le \|f\|^2$. The central challenge is defining an appropriate function space structure where $f$ lives, and where the Bessel inequality holds. It seemed to me that $f$ is not in structures like $L^2(\mathbb{R})$ or Besicovitch spaces $B^2$ (which I don't understand fully, more detail here), even under boundness assumption, but maybe I'm mistaken.

EDIT:

As noted in @conrad's amazing answer, establishing unboundedness hinges on showing that $c_k = \lim_{T\to\infty} \langle f, \psi_k \rangle_T = \lim_{T\to\infty} \frac{1}{T}\int_{0}^T f(x) \psi_k(x)dx = (-1)^{k+1}/2$.

I wanted to add that this can be justified without Kuzmin-Landau (that is still a nice inequality that I encourage you to study), instead using the uniform convergence and swapping the limit and sum, $ \lim_{T\to\infty} \sum_{j=1}^\infty (-1)^{j+1} \langle \psi_j, \psi_k \rangle_T = \sum_{j=1}^\infty (-1)^{j+1} \lim_{T\to\infty} \langle \psi_j, \psi_k \rangle_T $, .

Specifically, by pairing adjacent terms $(j=2m-1, 2m)$ in the series, we analyze the difference $ \langle \psi_{2m-1}, \psi_k \rangle_T - \langle \psi_{2m}, \psi_k \rangle_T $. It can be shown that $\langle \psi_j, \psi_k \rangle_T = \frac{1}{2} [\text{sinc}(T\frac{k-j}{jk}) - \text{sinc}(T\frac{k+j}{jk})]$. Applying the Mean Value Theorem on the interval $[1/(2m), 1/(2m-1)]$ to the function $y \mapsto \frac{1}{2}[\text{sinc}(T(y-1/k)) - \text{sinc}(T(y+1/k))]$ yields (for $2m-1 \ge 2k$): $$ |\langle \psi_{2m-1}, \psi_k \rangle_T - \langle \psi_{2m}, \psi_k \rangle_T| \le \frac{3k}{(2m-1)(2m)}. $$ This bound is crucially independent of $T$ and summable. By the Weierstrass M-test, the paired series $\sum_{m=1}^\infty [\langle \psi_{2m-1}, \psi_k \rangle_T - \langle \psi_{2m}, \psi_k \rangle_T]$ converges uniformly in $T$, rigorously permitting the interchange of limit and summation needed to find $ c_k = (-1)^{k+1}/2 $.

Question on Growth Rate:

@conrad suggested the behavior might be related to the Dirichlet divisor problem, hinting at $\sup_{|t| \le x} |f(t)| = \Omega(x^{1/4})$ as a lower bound and possibly $O(x^\epsilon)$ with $\epsilon$ not to far from $1/4$ as an upper bound. I have proved in my answer that: $$\sup_{|y| \le x} |f(y)| = \Omega(x^{1/4}/\ln(x)^{1/4})$$ Meaning that at least $\epsilon \ge 1/4$. Using tools from Graham and Kolesnik suggested by @conrad, I think it's possible to get $f(x)=O(x^{5/12})$ but it's far from $1/4$ (or more realistically $131/416$, the current upper bound for the dirichlet divisor problem).

Using acceleration formula (derived in this related question) combined with NUFFT (I used finufft package in python) allows for efficient numerical computation of $f(x)$ on a grid and thus its supremum $M(x)=\sup_{t \le x} |f(t)|$ over large ranges as shown in the plot below. Numerical analysis confirm @conrad suggestion.

Answer 1

I will give a proof that $f$ is unbounded though I strongly believe that one should be able to show that $f(x)$ is $\Omega(x^{1/4})$ (so there is $x_n \to \infty, |f(x_n)|>>x_n^{1/4}$) and the right order is most likely $1/4$ and $f(x)=O(x^{1/4+\epsilon})$ but this is related to the well-known Dirichlet divisor problem for which the $1/4+\epsilon$ upper bound is not known though it is known that $1/4$ is a lower bound but the proof is not trivial.

Anyway coming back to the problem it is enough show that $$\frac{1}{T}\int_0^Tf(x)\sin (x/k) dx \to (-1)^{k+1}/2$$ when $T\to \infty$ since then fixing a large $N$ and taking $g_N(x)=f(x)-\sum_{1\le k \le N}(-1)^{k+1}\sin (x/k)=f(x)-h_N(x)$ a direct computation shows that $$\int_0^T g_N(x)^2dx=\int_0^T (f(x)^2+h_N(x)^2-2\sum_{k=1}^N (-1)^{k+1}f(x)\sin (x/k)) dx$$

Dividing by $T$ and using the claim above we get $$0 \le \limsup_{T\to \infty}\frac{1}{T}\int_0^T f(x)^2dx-N/2$$ since a standard computation by squaring, expanding the sine products into a sum of two cosines (with coefficient $1/2$) and integrating term by term gives $$\frac{1}{T}\int_0^T h_N(x)^2dx=N/2+o(1)$$

Picking a large enough $N$ this contradicts the boundness of $f$

We will now sketch the proof of the claim. First we fix $k\ge 1$ and a large $T>(2k)^2$ and by uniform convergence on compacts of the partial sums of $f$ we can pick a large $M$ (depending on $T$ and which we can choose $>T$ wlog) st $|f_M-f|< \epsilon$ for all $0\le x \le T$ so replacing $f$ by $f_M$ in the averaged integral above gives an $\epsilon$ error since $|\sin x/k| \le 1$ and choosing $\epsilon =1/T$ for example we are good here.

Expanding the terms of $f_M\sin x/k$ into a cosine sum and integrating we get precisely one term (for $m=k$) that is $(-1)^{k+1}/2$ and a sum ($m=1 \cdots M$) of terms $\frac{\sin (T/k\pm T/m)}{1/k\pm 1/m}$ with alternating coefficients $\pm 1/2$ in $m$ and of course skipping the $m=k$ term for the $1/k-1/m$ term

We will show that both sums above are $o_k(T)$ proving the claim. We will do just $$\frac{1}{2}\sum_{m=1, m \ne k}^M(-1)^{m+1} \frac{\sin (T/k-T/m)}{1/k-1/m}=o(T)$$ as the other case is similar and actually easier.

We split the sum in $m<2k, 2k\le m < T^{2/3}, T^{2/3}\le m \le M$

The first sum is easy since $|\frac{1}{1/k-1/m}|=\frac{km}{|k-m|} \le 2k^2$ and $|sin \le 1|$) while the number of terms is at most $2k$ so the first sum is at most $4k^3=O_k(1)=o_k(T)$ as $k$ is fixed.

The second is also easy since we majorize the denominator by $1/(2k)$ (now $m\ge 2k$) so each term is at most that and there are $O(T^{2/3})$ terms so again we get an $o_k(T)$

For the last sum we expand $\sin (T/k-T/m)=\sin T/k \cos T/m-\cos T/k \sin T/m$ take the constants $\sin, \cos T/k$ in front and first look at the corresponding alternating cosine and sine sums without the denominator $1/k-1/m$ weight.

These are $\sum_{T^{2/3}\le m \le M}(-1)^{m+1}\cos T/m$ and the sine analog so we can just treat $$\sum (-1)^{m+1}e^{iT/m}=\sum e^{(2\pi i)((m+1)/2+T/(2\pi m))} $$ to deal with both.

But note that the derivative $y\to T/(2\pi y)+y/2$ is $1/2-T/(2\pi y^2)$ and is between $1/4$ and $1/2$ for $y\ge T^{2/3}$ and $T>1000$ say which of course we assume wlog too.

This means that all the sums $\sum_{T^{2/3}\le m \le M_1 \le M} (-1)^{m+1}e^{iT/m}$ are $O(1)$ independently of $T,M, M_1$ by Kuzmin-Landau.

Using that $1/(1/k-1/m)$ is decreasing and between $2k$ and $k$, summation by parts gives that the weighted alternated sum is indeed $O_k(1)=o_k(T)$ and we are done!

Answer 2

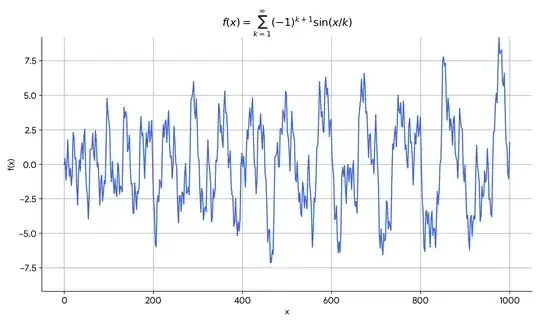
Looking at the zero of $f$, I had to prove a stronger quantitative result about its growth rate. Specifically, that the weighted integral $\int_1^\infty |f(x)|/x \, dx$ diverges. In order to do so, I proved a result that also confirmed @Conrad intuition that $f(x) = O(x^\epsilon)$ is only possible for $\epsilon \ge 1/4$.

Result: There exists a positive constant $c$ such that for all sufficiently large $T$, the function $f(x)$ satisfies the inequality: $$ \int_0^T f(x)^2 dx \ge \frac{c T^{3/2}}{\sqrt{\ln T}} $$

The Proof Strategy

The proof quantifies the argument from contradiction. Instead of taking limits as $T \to \infty$, we analyze the behavior for finite $T$ and a carefully chosen (large) integer $N$.

Let $\psi_k(x) = \sin(x/k)$ and define the partial sum $S_N(x) = \sum_{k=1}^N (-1)^{k+1} \psi_k(x)$. We use the time-averaging inner product $\langle g, h \rangle_T = \frac{1}{T}\int_0^T g(x)h(x) dx$.

Since the integral of a non-negative function is non-negative, we have: $$ \langle f - S_N, f - S_N \rangle_T \ge 0 $$ Re-arranging the terms we can get this lower bound for the mean-square of $f$: $$ \frac{1}{T}\int_0^T f(x)^2 dx \ge \langle S_N, S_N \rangle_T + 2\langle f-S_N, S_N \rangle_T $$ The core of the proof is to find a sharp lower bound for the right-hand side.

Bounding Tools

1. Paired Term Bound: Let $g(y) = \frac{1}{2}[\text{sinc}(T(y-1/k)) - \text{sinc}(T(y+1/k))]$, so that $\langle \psi_j, \psi_k \rangle_T = g(1/j)$. For $2m-1 \ge 2k$, we apply the Mean Value Theorem to $g(y)$ on the interval $[1/(2m), 1/(2m-1)]$: $$ |\langle \psi_{2m-1}, \psi_k \rangle_T - \langle \psi_{2m}, \psi_k \rangle_T| = |g(\frac{1}{2m-1}) - g(\frac{1}{2m})| = |g'(c)| \cdot \frac{1}{(2m-1)(2m)} $$ for some $c \in (\frac{1}{2m}, \frac{1}{2m-1})$. The derivative is $g'(y) = \frac{T}{2}[\text{sinc}'(T(y-1/k)) - \text{sinc}'(T(y+1/k))]$. Using $|\text{sinc}'(x)| \le 2/|x|$ for large $|x|$ and noting that for $y \in [1/(2m), 1/(2m-1)]$ and $2m-1 \ge 2k$, we have $|T(y-1/k)| \ge T/(2k)$ and $|T(y+1/k)| \ge T/k$. Thus, $|g'(c)| \le \frac{T}{2}(\frac{2}{T/(2k)} + \frac{2}{T/k}) = \frac{T}{2}(\frac{4k}{T}+\frac{2k}{T}) = 3k$. This gives the final bound: $$ |\langle \psi_{2m-1}, \psi_k \rangle_T - \langle \psi_{2m}, \psi_k \rangle_T| \le \frac{3k}{(2m-1)(2m)} $$

2. Dot product bound: For $j \ne k$, the integral is $T\langle \psi_j, \psi_k \rangle_T = \frac{1}{2}\left(\text{sinc}(T(\frac{1}{j}-\frac{1}{k})) - \text{sinc}(T(\frac{1}{j}+\frac{1}{k}))\right)$. Using the triangle inequality and $|\text{sinc}(x)| \le 1/|x|$ for $x \ne 0$: $$ T|\langle \psi_j, \psi_k \rangle_T| \le \frac{1}{2}\left(|\text{sinc}(T\frac{k-j}{jk})| + |\text{sinc}(T\frac{k+j}{jk})|\right) \le \frac{1}{2}\left(\frac{jk}{|k-j|} + \frac{jk}{k+j}\right) \le \frac{jk}{|k-j|} $$

3. Harmonic Sum Bound: This is a summed version of the Dot product bound. Because of symmetry we have $\sum_{k,j=1, k\ne j}^L \frac{kj}{|k-j|}= 2 \sum_{k=2}^L k \sum_{j=1}^{k-1} \frac{j}{k-j}$. Re-indexing the inner sum with $l=k-j$ gives $\sum_{l=1}^{k-1} \frac{k-l}{l} = kH_{k-1} - (k-1)$. The total sum is $2 \sum_{k=2}^L (k^2 H_{k-1} - k(k-1))$. Using the standard inequality $H_{n} < \ln(n) + 1$ and bounding the sums, one can establish an explicit upper bound. For $L \ge 2$, a safe and practical bound is given by: $$ T\sum_{k,j=1, k\ne j}^L |\langle \psi_j, \psi_k \rangle_T| \le \sum_{k,j=1, k\ne j}^L \frac{kj}{|k-j|} \le \frac{2L^3 \ln L}{3} + L^3 $$

The Main Calculation

To connect our strategy to the errors, we first expand the term $\langle S_N, S_N \rangle_T$: $$ \langle S_N, S_N \rangle_T = \sum_{j,k=1}^N (-1)^{j+k} \langle \psi_j, \psi_k \rangle_T = \sum_{k=1}^N \langle \psi_k, \psi_k \rangle_T + \sum_{j \ne k, j,k \le N} (-1)^{j+k} \langle \psi_j, \psi_k \rangle_T $$ The diagonal terms are $\langle \psi_k, \psi_k \rangle_T = \frac{1}{2} - \frac{k}{4T}\sin(\frac{2T}{k})$. Summing these from $k=1$ to $N$ gives $\frac{N}{2} + \sum_{k=1}^N \frac{k}{4T}\sin(\frac{2T}{k})$. The inequality $\frac{1}{T}\int_0^T f(x)^2 dx \ge \langle S_N, S_N \rangle_T + 2\langle f-S_N, S_N \rangle_T$ becomes: $\frac{1}{T}\int_0^T f(x)^2 dx \ge \frac{N}{2} + E_1(N,T) + E_2(N,T) + E_3(N,T)$ where:

• $E_1(N,T) = \sum_{k=1}^N \frac{k}{4T}\sin(\frac{2T}{k})$
• $E_2(N,T) = \sum_{j \ne k, j,k \le N} (-1)^{j+k} \langle \psi_j, \psi_k \rangle_T$
• $E_3(N,T) = 2\langle f-S_N, S_N \rangle_T = 2\sum_{k=1}^N (-1)^{k+1} \sum_{j=N+1}^\infty (-1)^{j+1} \langle \psi_j, \psi_k \rangle_T$

Our inequality becomes: $$\int_0^T f(x)^2 dx \ge \frac{NT}{2} - T|E_1(N,T)| - T|E_2(N,T)| - T|E_3(N,T)| $$

Bounding the Errors:

$T|E_1(N,T)| \le \sum_{k=1}^N \frac{k}{4} = \frac{N(N+1)}{8}$. This is negligible.

$T|E_2(N,T)| \le T\sum_{j \ne k, j,k \le N} |\langle \psi_j, \psi_k \rangle_T|$. Using Bounding Tool 3 (the Harmonic Sum Bound), this is bounded by $\frac{2N^3\ln N}{3} + N^3$.

$T|E_3(N,T)|$: We use a hybrid approach. We introduce a global integer cutoff $J > N$, which will be chosen optimally later (it will be of order $\sqrt{T}$ while $N$ of order $\sqrt{T/\ln T}$). The sum over $j$ is split into a "head" ($N<j<J$) and a "tail" ($j \ge J$). $$ T|E_3(N,T)| \le 2T \sum_{k=1}^N \sum_{j=N+1}^{J-1} |\langle \psi_j, \psi_k \rangle_T| + 2T \left| \sum_{k=1}^N (-1)^{k+1} \sum_{j=J}^{\infty} (-1)^{j+1} \langle \psi_j, \psi_k \rangle_T \right| $$

Tail Part: We choose $J \ge 2N+2$ so that Bounding Tool 1 (the Paired Term Bound) applies for all $k \le N$. Pairing terms in the sum over $j$ yields a bound independent of $T$: $$ T|\text{Tail}| \le 2T \sum_{k=1}^N \sum_{m=\lceil J/2 \rceil}^\infty \frac{3k}{(2m-1)(2m)} \le 6T \left(\sum_{k=1}^N k\right) \left(\sum_{m=\lceil J/2 \rceil}^\infty \frac{1}{m(m-1)}\right) $$ The inner sum is a telescoping series equal to $\frac{1}{\lceil J/2 \rceil-1} \le \frac{2}{J-2}\le \frac{3}{J}$ for $J$ large enough. $$ T|\text{Tail}| \le 6T \frac{N(N+1)}{2} \frac{2}{J-2} \le 9T \frac{N(N+1)}{J}$$

Head Part: For terms where $N<j<J$, we use Bounding Tool 2 (Dot product bound) and sum over the precise region. $$ T|\text{Head}| \le 2 \sum_{k=1}^N \sum_{j=N+1}^{J-1} \frac{jk}{|j-k|} = 2 \sum_{k=1}^N k \sum_{j=N+1}^{J-1} \frac{j}{j-k} $$ We analyze the inner sum: $\sum_{j=N+1}^{J-1} \frac{j}{j-k} = \sum_{j=N+1}^{J-1} (1 + \frac{k}{j-k}) = (J-N-1) + k \sum_{l=N+1-k}^{J-1-k} \frac{1}{l}$. This is bounded by $(J-N) + k \ln(\frac{J-k}{N-k+1}) \le J + k \ln(J)$. Summing over $k$ gives: $$T|\text{Head}| \le 2\sum_{k=1}^N (kJ + k^2\ln J) = J N(N+1) + \frac{N(N+1)(2N+1)}{3}\ln J$$

Now we combine the errors for $E_3$. The total error from this term is bounded by: $$ T|E_3(N,T)| \le J N(N+1) + \frac{9T N(N+1)}{J} + \frac{N(N+1)(2N+1)}{3}\ln J $$ To minimize the sum of the first two terms, which depend on our choice of $J$, we balance them by setting $J N(N+1) \approx 9T N(N+1)/J$. This implies $J^2 \approx 9T$, so we make the optimal choice $J = \lfloor 3\sqrt{T} \rfloor$. With this choice, for large $T$: $$ J N(N+1) \le 3\sqrt{T} N(N+1) \quad \text{and} \quad \frac{9T N(N+1)}{J} \le 4\sqrt{T} N(N+1) $$ Their sum is $7\sqrt{T}N(N+1)$. The logarithm term becomes $\ln J \le \ln(3\sqrt{T}) \le \ln T$ for large $T$. Substituting these into the bound for $T|E_3(N,T)|$ gives: $$ T|E_3(N,T)| \le 7\sqrt{T}N(N+1) + \frac{N(N+1)(2N+1)}{3}\ln T $$

Optimization and Conclusion

We have established the inequality: $$ \int_0^T f(x)^2 dx \ge \frac{NT}{2} - \sum_i T|E_i| $$

We wish to show that for an appropriate choice of $N$, this error is smaller than the main term $\frac{NT}{2}$. Let us choose $N = \left\lfloor\sqrt{\frac{T}{8\ln T}}\right\rfloor$. For sufficiently large $T$, this implies $N \ge 1$ and $N > \frac{1}{\sqrt{2}}\sqrt{\frac{T}{8\ln T}}$.

Upper Bound for the Error Term:

Using the bounds from the previous sections, the total error is bounded by: $$ \sum_i T|E_i| \le \frac{N(N+1)}{8} + \left(\frac{2N^3\ln N}{3} + N^3\right) + \left(7\sqrt{T}N(N+1) + \frac{N(N+1)(2N+1)}{3}\ln T\right) $$

We use the inequalities $N \le \sqrt{\frac{T}{8\ln T}}$ and $\ln N \le \frac{1}{2}\ln T$ (for large $T$). Let's bound the sum of errors, adding some $>1$ factors to simplify expressions for large $N, T$ : $$ \sum_i T|E_i| \le \frac{N^2}{4} + N^3 + 14\sqrt{T}N^2 + \frac{4}{3} N^3\ln T $$ The dominant term is the last one. Let's bound it: $$\frac{4}{3} N^3\ln T \le \left(\frac{T}{8\ln T}\right)^{3/2}\ln T = \frac{1}{12\sqrt{2}} \frac{T^{3/2}}{\sqrt{\ln T}} $$ The other terms are of a lower order. For instance, $14\sqrt{T}N^2 \le 14\sqrt{T}\frac{T}{8\ln T} = \frac{7}{4}\frac{T^{3/2}}{\ln T}$. For large $T$, the sum of these sub-dominant terms is much smaller than the dominant error term. A generous but safe bound for the total error for large $T$ is $\sqrt{2}$ the dominant part: $$ \sum_i T|E_i| \le \sqrt{2} \cdot \frac{1}{12\sqrt{2}} \frac{T^{3/2}}{\sqrt{\ln T}} = \frac{1}{12} \frac{T^{3/2}}{\sqrt{\ln T}} $$

Lower Bound for the Main Term: $$ \frac{NT}{2} > \frac{1}{2}\left(\frac{1}{\sqrt{2}}\sqrt{\frac{T}{8\ln T}}\right)T = \frac{T^{3/2}}{8\sqrt{\ln T}} $$

Final Inequality: Combining the lower bound for the main term and the upper bound for the error gives: $$ \int_0^T f(x)^2 dx \ge \frac{T^{3/2}}{8\sqrt{\ln T}} - \frac{1}{12} \frac{T^{3/2}}{\sqrt{\ln T}}=\frac{1}{24}\frac{T^{3/2}}{\sqrt{\ln T}} $$ Since $c = \frac{1}{24} > 0$, we have proven that for all sufficiently large $T$, the integral is bounded below as required. This completes the proof.

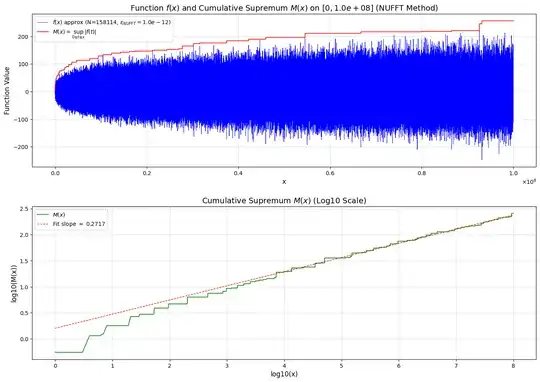
Implications for possible $\epsilon$ such that $f(x)=O(x^\epsilon)$ and $\sup_{|y| \le x} |f(y)|$

This result provides important lower bound on the growth exponent. Indeed, y the proven inequality: $c \sqrt{\frac{T}{\ln T}} \le \frac{1}{T} \int_0^T f(x)^2 dx \le \left(\sup_{|t| \le T} |f(t)|\right)^2$. Implying directly that: $$\sup_{|t| \le x} |f(t)| = \Omega(x^{1/4}/\ln(x)^{1/4})$$ This proves that the growth exponent of $f(x)$ cannot be less than $1/4$. Combining this with the elementary upper bound $f(x) = O(\sqrt{x})$ (from pairing terms), we can conclude that $f(x) = O(x^\epsilon)$, the optimal exponent lying in the range $[1/4, 1/2]$.

Divergence of the Weighted Integral $\int |f(x)|/x \, dx$

The main result on the mean-square lower bound provides the necessary tool to prove the divergence of $\int_1^\infty |f(x)|/x \, dx$. The proof is a consequence of the conflict between the mean-square lower bound and the elementary growth upper bound $f(x)=O(\sqrt{x})$. We proceed by contradiction.

1. Assume the integral $\int_1^\infty \frac{|f(x)|}{x} dx$ converges.

2. From the elementary bound $f(x) = O(\sqrt{x})$, there exists a constant $K$ such that $|f(x)| \le K\sqrt{x}$ for $x \ge 1$. This implies the inequality $\frac{f(x)^2}{x^{3/2}} \le K \frac{|f(x)|}{x}$. By the comparaison, the convergence assumed in step 1 implies that the integral $\int_1^\infty \frac{f(x)^2}{x^{3/2}} dx$ must also converge.

3. We now show this conclusion is incompatible with the mean-square lower bound. We use integration by parts on the integral $\int_1^T \frac{f(x)^2}{x^{3/2}} dx$, relating it to the energy integral $S(T) = \int_0^T f(x)^2 dx$. Using the lower bound $S(t) \ge \frac{c t^{3/2}}{\sqrt{\ln t}}$ for $t \ge t_0$, the integration by parts formula $\int_1^T \frac{S'(t)}{t^{3/2}} dt = \left[\frac{S(t)}{t^{3/2}}\right]_1^T + \frac{3}{2}\int_1^T \frac{S(t)}{t^{5/2}} dt$ yields a lower bound for $\int_1^T \frac{f(x)^2}{x^{3/2}} dx$ that involves the integral $\int_{t_0}^T \frac{1}{t\sqrt{\ln t}} dt$. This integral is known to diverge (its antiderivative is $2\sqrt{\ln t}$). Since all terms in the integration by parts formula are non-negative for large $t$, the divergence of this term implies that $\int_1^\infty \frac{f(x)^2}{x^{3/2}} dx$ must diverge. However, from step 2, we concluded this integral must converge. This is a contradiction. Thus, the assumption is false and $\int_1^\infty \frac{|f(x)|}{x} dx$ diverges.

4. The framework of this proof can be generalized. Assuming we have a better upper bound $f(x) = O(x^\alpha)$ for some $\alpha < 1/2$, the mean-square lower bound allows us to establish two stronger quantitative results. First that $\int_0^T |f(x)|dx = \Omega(T^{3/2-\alpha}/\sqrt{\ln T})$ and second, the weighted integral $\int_1^\infty \frac{|f(x)|}{x^{3/2-\alpha}} dx$ must diverge.

Note that @Conrad in his answer to an other question regarding the zeros of f has also proved $\int |f(x)|/x \, dx$ diverges with a simpler argument based "only" on the weaker result proved in his answer to this current question: $\frac{1}{T}\int_0^Tf(x)\sin (x/k) dx \to (-1)^{k+1}/2$ impliying $1/4 \le \frac{1}{T}\int_T^{2T}f(x)\sin x dx \le \frac{2}{2T}\int_T^{2T} |f(x)| dx \le 2\int_T^{2T} \frac{|f(x)|}{x} dx$ and the divergence.