In order to compute $\cos(\sin^{-1}(x))$ or $\sin(\cos^{-1}(x))$, all one has to do is draw an appropriate triangle to find that $$\cos(\sin^{-1}(x))=\sqrt{1-x^2}=\sin(\cos^{-1}(x)).$$ Using algebra, one can find that $\cosh(\sinh^{-1}(x))=\sqrt{x^2+1}$ and $\sinh(\cosh^{-1}(x))=\sqrt{x^2-1}$. Is there a simple geometric picture we can draw in order to conclude these facts about hyperbolic trig functions that doesn't rely on triangles with imaginary angles or side lengths (since we could just write $\sinh$ and $\cosh$ in terms of $\cos,\sin,i$)?
- 1,675
-
3this is a nice question – Jesse Madnick Mar 20 '25 at 15:55
-
2One could do so using the geometric definitions of hyperbolic functions (see this post, for instance, for more on that). – Ben Grossmann Mar 20 '25 at 15:56
-
Thanks! I did take a quick look about how $\cosh$ and $\sinh$ relate to the area of "that hyperbolic triangle" but it's not clear to me how to get inverse functions from there or how to take composition of hyperbolic and inverse hyperbolic from that picture. I guess I didn't think enough about that yet, thanks. – Maxim Gilula Mar 20 '25 at 15:57
-
2$\tanh x$ and $\operatorname{sech} x$ form a regular unit hypotenuse right triangle. Use the same ratio logic you use for regular trig to define the relations you want. – Ninad Munshi Mar 20 '25 at 15:57
-
@NinadMunshi that's a great idea. – Maxim Gilula Mar 20 '25 at 16:01
-
1The problem is that the "geometry" of $\cosh x$ and $\sinh x$ is not symmetric. The pairs $(u,v)=(\cosh x,\sinh x)$ are the points points of a hyperbola $u^2-v^2=1.$ So if you know $u$ then $v=\sqrt{u^2-1}$ and if you know $v$ then $u=\sqrt{1+v^2}.$'Imsuppose $u^2=1+v^2$ gives you a right triangle with one leg $1$ instead of hypotenuse $1.$ – Thomas Andrews Mar 20 '25 at 16:16
-
So if $\theta=\arctan(\sinh x)$ then $\cosh x=\sec\theta$ – Thomas Andrews Mar 20 '25 at 16:20
-
@ThomasAndrews It's ok if it's not symmetric, to me that just implies $\cosh(\sinh^{-1}(x))\neq \sinh(\cosh^{-1}(x))$. – Maxim Gilula Mar 20 '25 at 16:21
2 Answers
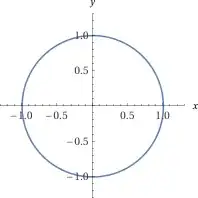
With regular trig (aka “circular”) functions, the parametric equation pair $(x(\theta) = \cos(\theta), y(\theta)= \sin(\theta))$ forms a circle centered at the origin, which can be expressed as $x^2 + y^2 = 1$.
Geometrically, $\sin(\cos^{-1}(t))$ asks “If you know that $x = t$ on the unit circle, what is $y$?” And $\cos(\sin^{-1}(t))$ asks “If you know that $y = t$ on the unit circle, what is $x$?” Both questions have the same answer, $\sqrt{1-t^2}$, due to the circle being symmetric.
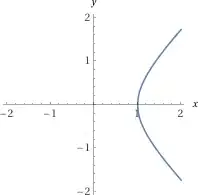
Similarly, from $x(\theta) = \cosh(\theta) = \frac{e^{\theta} + e^{-\theta}}{2}$ and $y(\theta) = \sinh(\theta) = \frac{e^{\theta} - e^{-\theta}}{2}$, it can be shown that $x^2 - y^2 = 1$. The graph of this equation forms a hyperbola (which, in case you didn't know, is the origin of the term “hyperbolic functions”). Actually, since the definition of $\cosh$ forces $x > 0$, you only get half of a hyperbola.
For your question, it doesn't matter what the parameter $\theta$ means geometrically (it's not the angle from the $x$ axis, which is $\arctan\left(1 - \frac{2}{e^{2\theta} + 1}\right)$), just how $x$ and $y$ are related to each other.
- $\sinh(\cosh^{-1}(t))$: Given $x = t$, what is $y$? It's $\sqrt{t^2 - 1}$.
- $\cosh(\sinh^{-1}(t))$: Given $y = t$, what is $x$? It's $\sqrt{t^2 + 1}$.
- 18,262
-
1Awesome! Thanks. Yes, I was focused too much on what the parameter represents, and this is a very clear and clean way to answer my question. – Maxim Gilula Mar 21 '25 at 05:26
$\tanh t$ and $\operatorname{sech} t$ form a right triangle of hypotenuse $1$ just like $\sin\theta$ and $\cos\theta$ do. Defining the following for a right triangle
$$\tanh t = \frac{\text{opp}}{\text{hyp}}$$
$$\operatorname{sech} t = \frac{\text{adj}}{\text{hyp}}$$
we get that
$$\sinh t = \frac{\text{opp}}{\text{adj}}$$
$$\cosh t = \frac{\text{hyp}}{\text{adj}} $$
Let's try an example. For $\sinh^{-1}(x)$ we label the opposite side as $x$ and the adjacent side as $1$ which leaves us with the hypotenuse as $\sqrt{1+x^2}$ and thus
$$\cosh\left(\sinh^{-1}(x)\right) = \frac{\sqrt{x^2+1}}{1} = \sqrt{x^2+1}$$
- 37,891
-
1
-
Beautiful! That's really helpful, thank you. That makes a lot of sense to have a right triangle since we also have a right triangle with side length $1,\sinh(t)$ and hypotenuse $\cosh(t)$. – Maxim Gilula Mar 20 '25 at 16:23
-
1Is there a nice way to create a diagram in mathjax without just uploading a photo from somewhere else? – Ninad Munshi Mar 20 '25 at 16:26
-
1Chatgpt and phind.com are good places to make diagrams quickly. Sometimes they don't do a good job, but sometimes they do a good job. – Maxim Gilula Mar 20 '25 at 16:28
-
2Wiki's graphic does the job IMO. There's also this interactive demonstration from Desmos. – user170231 Mar 20 '25 at 19:35