Why is the set $\{ (x,y,z) \geq 0: 3(xy+yz+xz) +1 \geq 2(x+y+z), x+y+z \leq 1\}$ convex?

Question

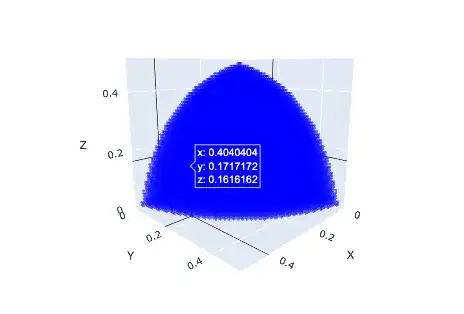
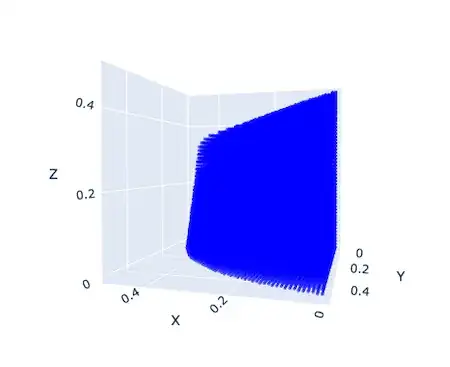
While trying to solve some problems, the following set

$$ S:= \{ (x,y,z): x,y,z \geq0 \} \cap \{ (x,y,z): 3(xy+yz+xz) +1 \geq 2(x+y+z) \} \cap \{ (x,y,z): x+y+z \leq 1 \} $$

showed up in my calculations and I needed to prove that this set is indeed convex.

Proving this directly seems to be quite hard, even for points on the boundary: Take two points $(a,b,c)$ and $(a',b',c')$ in $S$ that satisfy the equation

$$ 3(xy+yz+xz) +1 = 2(x+y+z) \tag{$\ast$}$$

we want to show that $ (1-t)(a,b,c) + t(a',b',c')$ is in $S$. Of course, we need to show only

\begin{align} 3\Big(((1-t)a+ta')((1-t)b+tb') &+ ((1-t)a+ta')((1-t)c+tc') + ((1-t)c+tc')((1-t)b+tb')\Big) + 1 \\ &\geq 2\Big( (1-t)(a+b+c) + t(a'+b'+c')\Big). \end{align} After simplifying (using $(*)$), this inequality is equivalent to

$$ (a-a')(b-b')+ (b-b')(c-c') +(c-c')(a-a') \leq 0, $$

and this is deadend. Any ideas?

Here are 3D plots of this set:

Answer 1

Fact 1. The set $$S := \{(x, y, z) : x, y, z \ge 0;\,\, x + y + z \le 1;\,\, 3(xy + yz + zx) + 1 \ge 2(x + y + z)\}$$ is convex.

Proof.

Let \begin{align*} T &:= \Big\{(x, y, z) : x, y, z \ge 0; \, x + y + z \le 1;\\ &\qquad\qquad\qquad 3(1 - x - y - z) \ge \sqrt{(3x-1)^2 + (3y-1)^2 + (3z-1)^2}\Big\}. \end{align*}

Then $S = T$ since \begin{align*} &6\cdot [3(xy + yz + zx) + 1 - 2(x + y + z)]\\ ={}& 9(1 - x - y - z)^2 - (3x - 1)^2 - (3y - 1)^2 - (3z - 1)^2. \end{align*}

It is easy to prove that $T$ is convex (noting that $3(1-x-y-z) \ge \|(3x-1, 3y-1, 3z-1)\|_2$ is convex).

Answer 2

Write $x=\frac{1}{3}-a$, $y=\frac{1}{3}-b$, $z=\frac{1}{3}-c$, and the inequalities become \begin{eqnarray} a b + b c + c a &\ge 0 \\ a+b+c &\ge 0 \end{eqnarray}

We could even prove that the subset of $\mathbb{R}^n$

\begin{eqnarray} \sum_{i=1}^n a_i &\ge 0\\ \sum_{i,j} a_i a_j& \ge 0 \end{eqnarray}

is convex. Now the quadratic form $\sum_{i,j} a_i a_j$ is negative definite on $\sum a_i = 0$ (could be seen as "equal distances $1$ between $n$ points in $\mathbb{R}^{n-1}$ ", or directly). Now this is analogous to the fact: the region ( light cone): $$\{(x_0, \ldots, x_{m}) \ | \ x_0^2-\sum_{i=1}^{m} x_i^2 \ge 0 \textrm{ and } x_0 \ge 0\}$$ is convex.

$\bf{Added}$ Let $V$ be a ($n$ dimensional) vector space over $\mathbb{R}$ ( or a totally ordered field) $Q$ a quadratic form on $V$ of signature $(1, n-1)$, $\phi$ a linear form on $V$ such that $Q$ is negative definite on the subspace $\{ \phi=0\}$. Then the set $\{Q> 0, \phi> 0\}$ is convex ( a convex cone). Indeed, consider $v$, $w$ in this set, non proportional. The restriction of $Q$ to the subspace by $v$, $w$ has signature $(1,-1)$ ( it cannot be $\preceq 0$). Now reduce to the case of $V$ of dimension $2$, where we can consider $Q= x_1^2-x_2^2$, and all is intuitive.