My question
Compute the following double integral analytically
$$\int_{-1}^1 \int_{-1}^1 2 \sqrt{x^2 y^2 - x^2 - y^2 + 1} \,\, \mathrm{d} x \mathrm{d} y$$
Background
The $3$-dimensional elliptope is the spectrahedron defined as follows
$$\mathcal E_3 := \Bigg\{ (x_{12}, x_{13}, x_{23}) \in \mathbb R^3 : \begin{bmatrix} 1 & x_{12} & x_{13}\\ x_{12} & 1 & x_{23}\\ x_{13} & x_{23} & 1\end{bmatrix} \succeq 0 \Bigg\}$$
Using Sylvester's criterion for positive semidefiniteness (i.e., all $2^3-1 = 7$ principal minors are nonnegative), we obtain $1 \geq 0$ (three times), the three quadratic inequalities
$$1 - x_{12}^2 \geq 0 \qquad \qquad \qquad 1 - x_{13}^2 \geq 0 \qquad \qquad \qquad 1 - x_{23}^2 \geq 0$$
and the cubic inequality.
$$\det \begin{bmatrix} 1 & x_{12} & x_{13}\\ x_{12} & 1 & x_{23}\\ x_{13} & x_{23} & 1\end{bmatrix} = 1 + 2 x_{12} x_{13} x_{23} - x_{12}^2 - x_{13}^2 - x_{23}^2 \geq 0$$
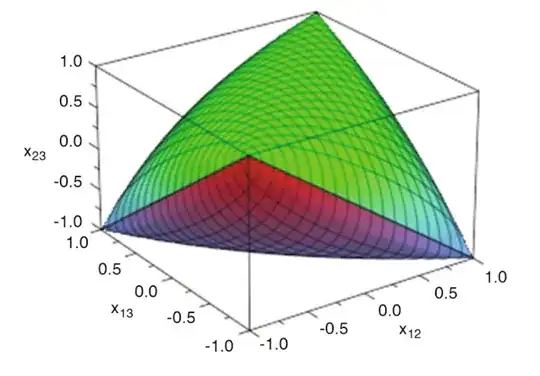
Thus, $\mathcal E_3$ is contained in the cube $[-1,1]^3$. Borrowing the pretty figure in Eisenberg-Nagy & Laurent & Varvitsiotis, here is an illustration of $\mathcal E_3$
What is the volume of $\mathcal E_3$?
Motivation
Why is $\mathcal E_3$ interesting? Why bother? Because $\mathcal E_3$ gives us the set of $3 \times 3$ correlation matrices.
My work
For convenience,
$$x := x_{12} \qquad\qquad\qquad y := x_{13} \qquad\qquad\qquad z := x_{23}$$
I started with sheer brute force. Using Haskell, I discretized the cube $[-1,1]^3$ and counted the number of points inside the elliptope. I got an estimate of the volume of $\approx 4.92$.
I then focused on the cubic surface of the elliptope
$$\det \begin{bmatrix} 1 & x & y\\ x & 1 & z\\ y & z & 1\end{bmatrix} = 1 + 2 x y z - x^2 - y^2 - z^2 = 0$$
which I rewrote as follows
$$z^2 - (2 x y) z + (x^2 + y^2 - 1) = 0$$
Using the quadratic formula, I obtained
$$z = x y \pm \sqrt{x^2 y^2 - x^2 - y^2 + 1}$$
Integrating using Wolfram Alpha,
$$\int_{-1}^1 \int_{-1}^1 2 \sqrt{x^2 y^2 - x^2 - y^2 + 1} \,\, \mathrm{d} x \mathrm{d} y = \cdots \color{gray}{\text{(magic happens)}} \cdots = \color{blue}{\frac{\pi^2}{2} \approx 4.9348}$$
I still would like to compute the double integral analytically. I converted to cylindrical coordinates, but did not get anywhere.
Other people's work
This is the same value Johnson & Nævdal obtained in the 1990s:
Thus, the volume is
$$\left(\frac{\pi}{4}\right)^2 2^3 = \frac{\pi^2}{2}$$
However, I do not understand their work. I do not know what Schur parameters are.
Haskell code
Here's the script:
-- discretization step
delta = 2**(-9)
-- discretize the cube [-1,1] x [-1,1] x [-1,1]
grid1D = [-1,-1+delta..1]
grid3D = [ (x,y,z) | x <- grid1D, y <- grid1D, z <- grid1D ]
-- find points inside the 3D elliptope
points = filter ((x,y,z)->1+2xyz-x2-y2-z*2>=0) grid3D
-- find percentage of points inside the elliptope
p = (fromIntegral (length points)) / (1 + (2 / delta))**3
After loading the script:
*Main> delta
1.953125e-3
*Main> p
0.6149861105903861
*Main> p*(2**3)
4.919888884723089
Hence, approximately $61\%$ of the grid's points are inside the elliptope, which gives us a volume of approximately $4.92$.
A new Buffon's needle
A symmetric $3 \times 3$ matrix with
$1$'s on the main diagonal
realizations of the random variable whose PDF is uniform over $[-1,1]$ on the entries off the main diagonal
is positive semidefinite (and, thus, a correlation matrix) with probability $\left(\frac{\pi}{4}\right)^2$. Estimating the probability, we estimate $\pi$. Using the estimate given by the Haskell script:
*Main> 4 * sqrt 0.6149861105903861
3.1368420058151125
References
Cynthia Vinzant, What is a... Spectrahedron?, Notices of the AMS, Volume 61, Number 5, May 2014.
Grigoriy Blekherman, Pablo A. Parrilo, Rekha R. Thomas, Semidefinite Optimization and Convex Algebraic Geometry, SIAM, March 2013.
Marianna Eisenberg-Nagy, Monique Laurent, Antonios Varvitsiotis, Complexity of the positive semidefinite matrix completion problem with a rank constraint, arXiv:1203.6602.
C. R. Johnson, G. Nævdal, The probability that a (partial) matrix is positive semidefinite, in Recent Progress in Operator Theory, International Workshop on Operator Theory and Applications, IWOTA 95, Regensburg, July 31–August 4, 1995.