Geometric interpretation of infinite tetration of $i$

Question

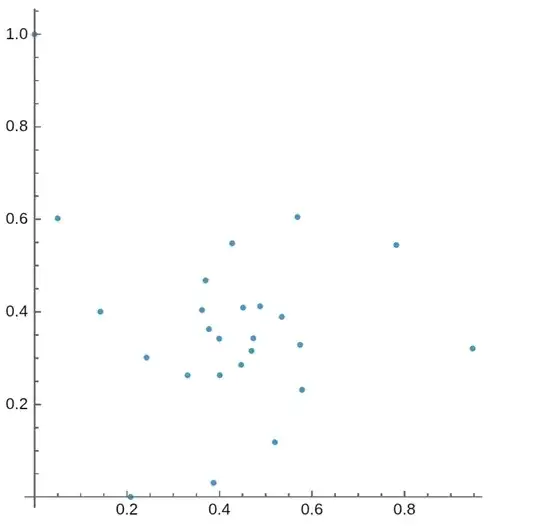
Plotting in the complex plane the sequence given by the tetration of $i$: $\{i, i^i, i^{i^i}, \ldots \} $, we can clearly notice that this plot has three spiral arms, as if there are three sequences converging in the point representing the infinite tetration of $i$, call it $c$.

If we consider three subsequent points inside this sequence, they can be seen as vertex of a triangle: is there any geometric property holded by $c$ respect to the triangle?

I considered the triangle with the vertex $\{i, i^i, i^{i^i}\}$, but the $c$ point doesn't represent any notable point (such as the centroid, incenter, circumcenter, or orthocenter)

Answer 1

If there is no obvious geometric relation between the triangle of three first terms $(i,i^i,i^{i^i})$ and $c$, you may study the asymptotic relation with the triangle given by three consecutive terms and $c$.

Since the logarithm is multivalued, I guess you use the recurrence function $f:z\mapsto \exp(zi\pi/2)$ to define your sequence. Around $c\approx 0,45+0,35i$, the derivative is $f'(c)=\frac{i\pi}2f(c)=\frac{i\pi c}2$ with an argument near $\frac{2\pi}{3}$. That’s why you see three spiral arms.

To get more information on $c=re^{i\theta}$ you get $$re^{i\theta}i\frac{\pi}2=\ln(r)+i\theta\iff\begin{cases}-r\frac{\pi}2\sin(\theta)=\ln(r)\\r\frac{\pi}2\cos(\theta)=\theta\end{cases}$$ Then $$-\theta\tan(\theta)=\ln(r)=\ln\left(\frac{\theta}{\frac{\pi}2\cos(\theta)}\right)$$ So $\theta$ is the unique fixed point of $t\mapsto\frac{\pi}2\cos(t)\exp(-t\tan(t))$ or $t\mapsto \frac{1}{\tan(t)}\ln\left(\frac{\pi\cos(t)}{2t}\right)$.