How would you describe a triangle with a sin 90 based on the definition of sine?

Question

I understand this problem is similar to the following question: How would a triangle for sin 90 degree look

However, I am confused on how sine 90 is defined based on the definition of sine: opposite/hypotenuse. There were two explanations I heard:

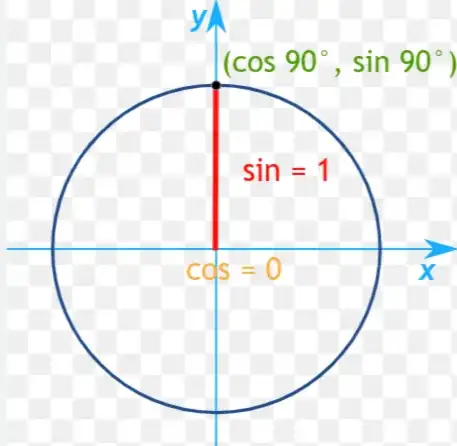
The first is that in a right triangle, the angle opposite the right angle is the same as the hypotenuse, so hypotenuse/hypotenuse=1. I used to be sure about this explanation, but then I heard that the opposite side or adjacent side cannot be the hypotenuse of a right triangle. Also, this does not seem to make sense in regards to a unit circle. In a unit circle, when finding the sine of an acute angle, the right angle is located opposite the origin:

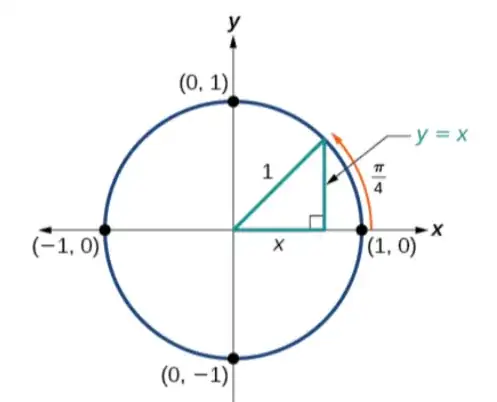
In the unit circle, the angle in the right triangle whose sine is being measured is located at the origin, which means when measuring sin 90 in a right triangle in the unit circle, there will be two right angles in the triangle, correct? From what I know this is not possible, so the triangle will sort of collapse into a line.

The unit circle explanation is that the opposite side gets larger and larger as the angle at the origin nears 90 degrees, while the adjacent side gets smaller and smaller, until the opposite side and the hypotenuse are the same (opposite side becomes equal to 1).

Essentially, the unit circle explanation seems easier to visualize, but is the first one still valid? The only reason I am asking this is because the first explanation seems to create a regular right triangle, but the second creates a triangle that is really just a line. Maybe this is a basic question and can be answered easily, but I am really confused on this. Hopefully the question makes sense, but if not, please let me know. Thanks.

Answer 1

The short answer to the question in the title is that there is no such triangle, so there is no need to decide how to describe it "based on the definition of sine".

A slightly longer answer is that there are two common definitions of the sine function. The one that's "opposite over hypotenuse" works for honest right triangles. The other is "the $y$ coordinate of a point on the circle". They give the same answer when both are defined. The second but not the first allows 90 degrees as an input value. You can see geometrically that the value of 1 for the sine there is the limiting value as one of the non-right angles in a right triangle approaches a right angle.

Answer 2

I have heard more than one person say that the sine and cosine should be considered as functions on the circle rather than the triangle. What does that mean?

As all of us were taught, we start with a right triangle. Since the three angles of a triangle must sum to $180^{\circ}$ and one of the angles is $90^{\circ}$, it must be the case that each of the other angles is less than $90^{\circ}$ because neither can be $0^{\circ}$.

We consider one of the non-right angles. We define the adjacent and opposite sides and then the trig functions based on the six possible ratios of the sides. This is well defined because these ratios hold for all similar triangles, i.e. triangles whose angles are the same.

We then consider a point $(x,y)$ on a circle of radius $r$ in the first quadrant with $x$ and $y$ positive. We notice that the values $x$, $y$ and $r$ form the sides of a right triangle and, moreover, we conclude that $$\sin{\theta}=\frac{y}{r}\\ \cos{\theta}=\frac{x}{r}$$ with respect to the angle $\theta$ that the hypotenuse makes with the $x$ axis.

We then extend the definition of the trig functions to any $x$ and $y$ on the circle by defining $$\sin{\theta}=\frac{y}{r}\\ \cos{\theta}=\frac{x}{r}\\ \tan{\theta}=\frac{y}{x}$$ and the cosecant, secant and cotangent, respectively, as the corresponding reciprocals.

Since we can think about a point on the circle as traveling around the circle in any direction, we can generate the familiar sine and cosine functions that are defined on the entire real line.

In this sense, we are not dividing the hypotenuse by itself when we compute $\sin{90^{\circ}}$, we are dividing the $y$ coordinate of $(0,r)$ by the radius $r$. Since these values are the same, we get that the sine of $90^{\circ}$ is $1$.

Answer 3

Such a triangle doesn't exist, but you can regard it as a limit.

Let ABC be a right angled triangle with sides

$$|AB| = x,\quad |BC| = \epsilon,\quad |CA|=\sqrt{x^2+\epsilon^2}$$

Let $\gamma = \angle BCA$, then

$$\sin \gamma = \frac{x}{\sqrt{x^2+\epsilon^2}}$$

If we now make the side $|BC|$ smaller and smaller, we can take a look at the following limit, given $x>0$.

$$\lim_{\epsilon\to 0}\frac{x}{\sqrt{x^2+\epsilon^2}} = \frac{x}{\sqrt{x^2}} = 1$$

From what I know this is not possible, so the triangle will sort of collapse into a line.

So this is precisely what happens.

Answer 4

It is easier to explore the intersection point between one angle's side and the circle, than the triangle itself. When the angle is $\vartheta$, the x-value is the adjacent side and the y-value is the opposite one, but since the radius of the circle is 1, we can say $\sin\vartheta=\frac H{OS}=\frac y1=y$, and $\cos\vartheta=\frac H{AS}=\frac x1=x$, so the coordinates of this intersection are $(\cos \vartheta; \, \sin \vartheta)$.

When $\vartheta=\frac{\pi}{2} \,rad=90°$, the triangle becomes a line. Your trick technicaly works, but now it's a line, and we need a triangle, so... we can't do that. Instead, qe can see our point at $(0;1)$, and thanks to our discovery, we know it means $\cos 90=0$ and $\sin 90=1$