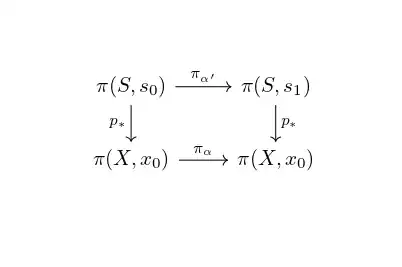Homomorphisms of Covering Spaces

Question

I am trying to find an example of a topological space admitting two non-isomorphic covering spaces $(S,p)$ and $(T,q)$ for which there exists a homomorphism $\phi$ of $(S,p)$ into $(T,q)$ and a homomorphism $\psi$ of $(T,q)$ into $(S,p)$ (see Note 1 below for the notation and terminology used here and for the implicit assumptions we make).

I am pretty sure such an example exists, but I could not find any up to now, so any help is welcome. Thank you very much in advance for your kind attention.

NOTE 1. All topological spaces in this post are assumed to be path connected and locally path connected, as it is usual in the theory of covering spaces.

For any topological space $X$ and any $x \in X$, the fundamental group of $X$ at the base point $x$ is denoted by $\pi(X,x)$. Given two spaces $X$ and $Y$, a continuous map $f:X \rightarrow Y$ and a point $x \in X$, we denote by $f_{*}:\pi(X,x) \rightarrow \pi(Y,f(x))$ the homomorphism defined by $f_{*}([\gamma])=[f \circ \gamma ]$ for any loop $\gamma$ at $x$.

If $\alpha:[0,1] \rightarrow X$ is a path in $X$, with $\alpha(0)=x_0$ and $\alpha(1)=x_1$, then $\pi_{\alpha}:\pi(X,x0) \rightarrow \pi(X,x_1)$ denotes the isomorphism defined by $\pi_{\alpha}([\gamma])=[(\alpha^{-1} \cdot \gamma) \cdot \alpha]$ for any loop $\gamma$ at $x_0$, where $\alpha^{-1}$ is the inverse path of $\alpha$, that is $\alpha^{-1}(s)=\alpha(1-s)$ for any $s \in [0,1]$, and for any two paths $\sigma$, $\tau$ in $X$ with $\sigma(1)=\tau(0)$, the product $\sigma \cdot \tau$ is defined by \begin{equation} (\sigma \cdot \tau) (s) = \begin{cases} \sigma(2s) & 0 \leq s \leq 1/2, \\ \tau(2s-1) & 1/2 \leq s \leq 1. \end{cases} \end{equation}

A covering space $(S,p)$ of a space $X$ consists of a topological space $S$ and a continuous surjective map $p:S \rightarrow X$ such that for any $x \in X$ there exists an open neighborhood $U$ of $x$ such that $p^{-1}(U)$ is the disjoint union of open sets, each of which is mapped homeomorphically by $p$ onto $U$. Given two covering spaces $(S,p)$ and $(T,q)$ of $X$ a homomorphism of $(S,p)$ into $(T,q)$ is a continuous map $\phi:S \rightarrow T$ such that $p=q \circ \phi$. A homomorphism $\phi$ of $(S,p)$ into $(T,q)$ is called an isomorphism of $(S,p)$ onto $(T,q)$ if $\phi$ is a homeomorphism of $S$ onto $T$. Two covering spaces $(S,p)$ and $(T,q)$ of $X$ are said to be isomorphic is there exists an isomorphism of one onto the other.

NOTE 2. In the example we are looking for $X$ must have a non-abelian fundamental group. Indeed, if $X$ has an abelian fundamental group, and $(S,p)$ and $(T,q)$ are covering spaces of $X$ for which there exists a homomorphism $\phi$ of $(S,p)$ into $(T,q)$ and a homomorphism $\psi$ of $(T,q)$ into $(S,p)$, then $(S,p)$ and $(T,q)$ turn out to be isomorphic, as the following argument shows.

Choose an arbitrary $s_0 \in S$ and put $t_0=\phi(s_0)$, $s_1=\psi(t_0)$, $x_0=p(s_0)$. We have $$p(s_1)=p(\psi(t_0))=q(t_0)=q(\phi(s_0))=p(s_0)=x,$$

so that $s_0,s_1 \in p^{-1}(x_0)$.We have $$ p_{*}(\pi(S,s_0))=q_{*}(\phi_{*}(\pi(S,s_0))) \subseteq q_{*}(\pi(T,t_0)), $$ and $$ q_{*}(\pi(T,T_0))=p_{*}(\psi_{*}(\pi(T,t_0))) \subseteq p_{*}(\pi(S,s_1)). $$ Let $\alpha':[0,1] \rightarrow S$ be a path such that $\alpha'(0)=s_0$ and $\alpha'(1)=s_1$, and put $\alpha= p \circ \alpha'$. It is easy to verify that the following diagram

commutes, so that the isomorphism $\pi_{\alpha}$ sends the subgroup $p_{*}(\pi(S,s_0))$ of $\pi(X,x_0)$ onto the subgroup $p_{*}(\pi(S,s_1))$. Now since $\pi(X,x_0)$ is abelian and $\alpha$ is a loop at $x_0$ it is easy to check that the isomorphism $\pi_{\alpha}$ is the identity map of $\pi(X,x_0)$, so that $p_{*}(\pi(S,s_0))=p_{*}(\pi(S,s_1))$. By using this fact and the two inclusions proved above we then get $p_{*}(\pi(S,s_0))=q_{*}(\pi(T,t_0))$. This last equality implies in turn the existence of an isomorphism $\theta$ of $(S,p)$ into $(T,q)$ such that $\theta(s_0)=t_0$ (see e.g. Fulton, Algebraic Topology, Corollary 13.6 or Massey, A Basic Course in Algebraic Topology, Chapter 5, Corollary 6.4). Hence $(S,p)$ and $(T,q)$ are isomorphic.

Answer 1

With the usual assumptions on $X$ so that covering space theory applies, this question is equivalent to the following group-theoretic question:

Can we find a group $G$ and two subgroups $H, K$ of $G$ which are not conjugate but such that $H$ is conjugate to a subgroup of $K$ and vice versa?

$G$ cannot be finite or abelian. We can take $G$ to be the Baumslag-Solitar group

$$BS(1, 4) \cong \langle a, b \mid bab^{-1} = a^4 \rangle \cong \mathbb{Z} \left[ \frac{1}{4} \right] \rtimes \mathbb{Z}$$

where in the semidirect product decomposition $\mathbb{Z}$ acts by conjugation by $b$, so acts by multiplication by $4$ on $\mathbb{Z} \left[ \frac{1}{4} \right]$, which is generated (under conjugation) by $a$, and we will take $H = \langle a \rangle, K = \langle a^2 \rangle$, which are abstractly isomorphic to $\mathbb{Z}$. $K$ is a subgroup of index $2$ in $H$, while the conjugate $bHb^{-1} \cong \langle a^4 \rangle$ is a subgroup of index $2$ in $K$.

To show that $H$ and $K$ are not conjugate it suffices to show that $a$ is not conjugate to either $a^2$ or $a^{-2}$. The Baumslag-Solitar relation can be used to rewrite every word $w \in G$ in $a, b$ by commuting all copies of $b$ to the right past copies of $a$, so that every word has a unique normal form $a^n b^m$. Now we can just compute the conjugation by this word, which gives

$$\begin{align*} waw^{-1} &= a^n b^m a b^{-m} a^{-n} \\ &= a^n a^{4^m} a^{-n} \\ &= a^{4^m} \end{align*}$$

which is never equal to $a^2$ or $a^{-2}$. (This requires that we really prove that words have unique normal forms, or we can use the linear representation $a \mapsto \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, b \mapsto \begin{bmatrix} 4 & 0 \\ 0 & 1 \end{bmatrix}$ into $GL_2(\mathbb{Z} \left[ \frac{1}{4} \right])$, which is faithful.)

To conclude, in case this needs to be said, every group is the fundamental group of a CW complex, and since $BS(1, 4)$ in particular can be defined by two generators and one relation, we can take this CW complex to have one $0$-cell, two $1$-cells, and one $2$-cell. So there even exists a very nice small CW complex $X$ with this fundamental group, and CW complexes are locally contractible so covering space theory applies to them, so the necessary covers also exist. We get that $X$ has two non-isomorphic covers which are each double covers of each other.

---

Edit: Here's an example where $G$ is much larger but admits many different variations, which hopefully conveys the point that this kind of behavior is robust. It was inspired by an incorrect but fixable example generated by Gemini 2.0 Flash Thinking Experimental.

We'll take $G = PL(\mathbb{R})$ to be the group of piecewise-linear homeomorphisms $\mathbb{R} \to \mathbb{R}$; these are either strictly increasing or strictly decreasing functions whose graphs in $\mathbb{R}^2$ can be drawn by drawing finitely many lines connected together. This is a large group but we can cut it down by requiring the breakpoints and slopes to be rational; it won't affect the argument either way. $G$ contains elements such as $x \mapsto ax + b, a \neq 0$ (these are the linear homeomorphisms) as well as elements such as

$$x \mapsto \begin{cases} 2x & \text{if } x \le 0 \\ 3x & \text{if } x \ge 0 \end{cases}.$$

For $f : X \to X$ a homeomorphism on a topological space, its support is the closure of its non-fixed points

$$\text{supp}(f) = \overline{ \{ x \in X : f(x) \neq x \} }.$$

So a homeomorphism with a given support $Y \subseteq X$ only "mixes around" $Y$ and leaves the complement alone. For any closed subspace $Y \subseteq X$, define the subgroup

$$G_Y = \{ g \in G : \text{supp}(g) \subseteq Y \}$$

of $G$ consisting of elements whose support is contained in $Y$. We have the following general observations about how these subgroups behave under conjugacy:

Proposition:

1. If $g \in G$, then $g G_Y g^{-1} = G_{gY}$.
2. If $Y_1 \subseteq Y_2$ then $G_{Y_1} \subseteq G_{Y_2}$.
3. If $G_{Y_1} = G_{Y_2}$ and $Y_1, Y_2$ are finite disjoint unions of closed intervals then $Y_1 = Y_2$.

Here we require closed intervals to have nonzero length. The first two are clear from the definitions and are true for $G$ a group of homeomorphisms on any topological space. For the third we can do it by showing that $G_Y$ contains an element $g$ whose support is exactly $Y$, so that $Y$ is the union of all supports of elements of $G_Y$. This can be done by an explicit construction for $Y$ a finite disjoint union of intervals; it suffices to take $g(x) = x$ for $x \not \in Y$ and for $g(x)$ to have no fixed points inside each interval, e.g. we can take

$$g(x) = \begin{cases} \frac{x}{2} & \text{ if } x \le \frac{1}{2} \\ \frac{3}{2}x-\frac{1}{2} & \text{ if } x \ge \frac{1}{2} \end{cases}$$

on the interval $[0, 1]$, and translate and stretch this example to cover a general interval.

Corollary: If $Y_1, Y_2 \subset \mathbb{R}$ are finite (non-empty) disjoint unions of intervals with different numbers of intervals, then

1. $G_{Y_1}$ and $G_{Y_2}$ are conjugate to subgroups of each other, but
2. $G_{Y_1}$ and $G_{Y_2}$ are not conjugate.

1 follows from the fact that a PL homeomorphism (in fact a linear homeomorphism) can send any finite disjoint union of intervals inside another interval together with part 1 and 2 of the proposition, while 2 follows from parts 1 and 3 of the proposition.

Now we can take, for example,

$$H = G_{[0, 1]}, K = G_{[0, 1] \cup [2, 3]}.$$

Gemini's incorrect example was $H$ as above but $K = G_{[0, 2]}$, which is conjugate to $H$. But this is fixable as we've seen!

The conceptual point here is that we reduce the question, roughly, to the observation that there exist topological spaces which are not homeomorphic but which are homeomorphic to subspaces of each other. We could replace $\mathbb{R}$ with other topological spaces with a "sufficiently rich" group of homeomorphisms (enough for some version of part 3 of the proposition to hold), for example $\mathbb{R}^n$, and consider various interesting closed subspaces to construct $H$ and $K$.

This example is actually not so distant from the example of the Baumslag-Solitar group $BS(1, 4)$, which in fact embeds into the group of linear homeomorphisms $\mathbb{R} \to \mathbb{R}$, with the embedding given by $a \mapsto (x \mapsto x + 1)$ and $b \mapsto (x \mapsto 4x)$.