Is the surface of a cone flat?

Question

I'll say it right away that I'm not familiar with math or Riemanian geometry, and what I'm seeking is more of an intuitive answer (although equations can help).

I know two things:

1. You can construct a conus by cutting away an angle at the apex and then glueing together the edges.
2. You can tell if you're on a flat surface by constructing a triangle and measuring the angles.

I wanted to do those things using pen and paper, and then measure the angles myself or at least try to see it visually, but realised one vital thing: I have no idea how to construct a geodesic on the cone. If I draw a straight line with a ruler before folding the paper into a cone, would it become a geodesic?

With my confusion I come to this forum: I want to know an (preferrably intuitive) answer to the question of whether the surface of a cone is flat or not. If someone can give an answer to an earlier question about geodesics that would be helpful as well.

Answer 1

A conical surface is indeed flat – except at the apex. That one point, with infinite curvature because planes tangent to the cone suddenly change orientation, is quite enough to throw you for a loop.

A little experiment: Start with a circular disk and draw a concentric square. Cut away the 90° sector that includes any side of the square and then glue the remaining 270° sector to make a cone. The remaining three sides of the square now close to make a geodesic equilateral triangle whose vertex angles are all 90° (the angle at the glued element is the sum of two 45° angles from the cut square).

Clearly this does not represent a flat-surface triangle whose angles should have summed to 180° instead of the 270° you actually got. Note that the 90° excess matches the angle you originally cut from the sector.

Imagine replacing the region around the apex with a small spherical surface tangent to the cone, like a pencil point becoming dull. The non-flat spherical surface is essentially a spreading-out of the apex singularity over a nonzero area. If you work out the area of this spherical surface in steradians, you get $\pi/2$ – matching the 90° excess angular sum you got from your original construction. This equality comes about because the vertices of the triangle are equidistant from the apex.

Answer 2

It depends what type of curvature (and hence what type of flatness) you're asking about.

A cone has no intrinsic curvature.  (Except at the apex — which is an exception to all the following points…)  Technically, the Gaussian curvature at any point is zero.  You can tell that because you can cut it open and unroll it into a flat surface without stretching or deforming it.  And, as you refer to, any triangle you draw on the cone (not containing the apex) has angles that add up to π (or, equivalently, 180°).  If you were an ant who lived inside the surface and knew nothing about the outside space, you wouldn't be able see any curvature.

However, a cone has extrinsic curvature when embedded in three-dimensional (or higher) space.  You can tell that because sections through it generally yield curves; the tangent direction varies across the surface — and because it looks curved to an external observer.

For more on those two types of curvature, see for example this question.

Answer 3

Your intuition is correct on both counts. The cone is "flat" and those are geodesics. The definitions and equations to support that need too much space for an answer here.

Answer 4

Unfortunately, there are several misconceptions in the posted answers stemming from the fact that the "usual" Riemannian geometry is ill-equipped to deal with non-smooth surfaces such as cones. The trouble is that Gaussian curvature as a function on a surface in the case of non-smooth surfaces no longer makes sense. This is why one gets paradoxical conclusions of the type "the surface is flat, but not really flat." There are several approaches on how to define curvature in the singular setting, which can be all traced to A.D.Alexandrov. The easiest one to explain is to treat Gaussian curvature not as a function but as a signed measure on the surface. Then the curvature of a cone will be a singular measure concentrated at a single point, namely, the tip of the cone. Physicists, of course, use such measures all the time, and, accordingly, measures supported at a single point $p$ are multiples of the Dirac measure $\delta_p$. (You may have heard of $\delta$-functions: This is what we are dealing with here.) In the case of a cone with the total surface angle $\theta$ (defined so that $\theta=2\pi -\alpha$, where $\alpha$ is as in tkf's answer) the curvature measure is $$ \alpha\delta_p. $$ This works not only for surfaces with zero curvature (away from singularities) but for general Riemannian metrics with conical singularities. It even makes sense if $\theta>2\pi$, in which case $$ \alpha=2\pi-\theta<0, $$ i.e. we get negative curvature measure. With this in mind, the usual Gauss-Bonnet formula for Riemannian metrics on compact surfaces $S$ (for simplicity, without boundaries) still works: $$ 2\pi \chi(S)=\int_S KdA, $$ where $KdA$ is understood as measure density: You integrate Gaussian curvature over the smooth part of the surface and then add $$ \sum_{j=1}^n \alpha_j, $$ the total curvature at (conical) singular points. For instance, if $S$ is the surface of a cube in Euclidean 3-space, you get eight singular points, each with the total angle $3\pi/2$. Then the Gauss-Bonnet formula reads $$ 2\pi \chi(S)=4\pi= \int_S KdA= \sum_{j=1}^8 \left(2\pi- \frac{3\pi}{2}\right)= \sum_{j=1}^8 \frac{\pi}{2}= 4\pi, $$ as expected.

This stuff (with suitable modifications) even works in higher dimensions, see e.g.

Troyanov, Marc, Les surfaces euclidiennes à singularités coniques. (Euclidean surfaces with cone singularities), Enseign. Math., II. Sér. 32, 79-94 (1986). ZBL0611.53035.

Adamowicz, Tomasz; Veronelli, Giona, Isoperimetric inequalities and geometry of level curves of harmonic functions on smooth and singular surfaces, Calc. Var. Partial Differ. Equ. 61, No. 1, Paper No. 2, 30 p. (2022). ZBL1480.30031.

Lott, John, Ricci measure for some singular Riemannian metrics, Math. Ann. 365, No. 1-2, 449-471 (2016). ZBL1343.53031.

To conclude: The cone is not flat, it has positive curvature measure concentrated at its tip.

Answer 5

Here is my attempt to blend intuition and formulas, to show explicitly that the identification of a piece of surface of the cone (away from the apex) with a piece of a flat plane, is distance preserving.

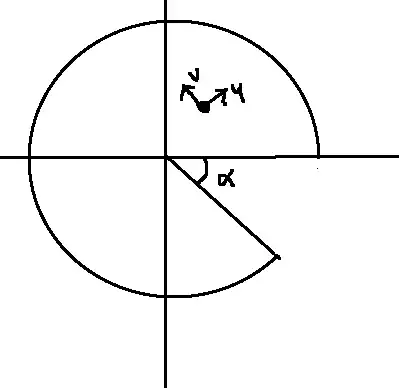
If we remove an $\alpha$ radian sector from a disk, we can it fold into a cone. Going from polar co-ordinates on the remaining disk $$0\leq r\leq 1,\\0\leq \theta\leq 2\pi-\alpha,$$ to cartesian co-ordinates on $\mathbb{R}^3$, this "folding map" may be written:

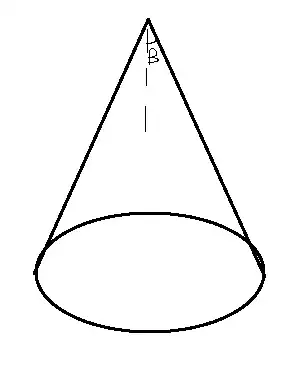
$$f\colon (r,\theta)\mapsto \left(r \sin\beta\cos\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right),r \sin\beta\sin\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right),-r\cos\beta\right).$$ Here $\sin\beta=\frac{2\pi-\alpha}{2\pi}$, and $\beta\in[0,\frac\pi2]$.

Intuitively, all this map does is send (what remains of) concentric circles on the disk to horizontal circles on the cone. As we have removed a sector from the disk, we need to speed up how fast we go round the cone, by a factor of $\frac{2\pi}{2\pi-\alpha}$, so as $\theta$ goes from $0$ to $2\pi-\alpha$, we go all the way round the cone. We incline the slope of the cone $\beta$, so that what remains of the circumference of the disk, equals the entire circumference of the corresponding circle on the cone.

It remains to verify that this map is distance preserving. Given a point $P$ on the disk, let $u$ be the outward facing radial tangent vector at $P$. Let $v$ be the unit anti-clockwise facing tangent vector at $P$. So $$u=\frac\partial {\partial r},\\v=\frac 1r\frac\partial{\partial \theta}.$$

Then $u,v$ form an orthonormal basis of the tangent space at $P$.

$f$" />

We just need to check that $f_*(u),f_*(v)$ form an orthonormal basis of the tangent space at $f(P)$. The reason this is sufficient, is that if a linear map $L\colon U\to V$ takes an orthonormal basis of $U$ to an orthonormal basis of $V$, then an arbitrary pair of vectors in $U$ may be written $\left(\begin{array}{c}a_1\\a_2\\\vdots\end{array}\right),\left(\begin{array}{c}b_1\\b_2\\\vdots\end{array}\right)$ with respect to the first basis, so their images in $V$ will be $\left(\begin{array}{c}a_1\\a_2\\\vdots\end{array}\right),\left(\begin{array}{c}b_1\\b_2\\\vdots\end{array}\right)$ with respect to the second basis. Thus in both cases the dot product of the vectors will be $a_1b_1+a_2b_2+\cdots$, as both basis' are orthonormal. So the map $L$ preserves norms. Once we know $f_*$ preserves norms, then we know $f$ preserves distance, as distances on a surface are obtained by integrating (along paths) norms in tangent spaces.

Intuitively $f_*(u)$ is just the unit vector of steepest descent down the cone. In formulas:

$$f_*(u)=\frac{\partial f}{\partial r}=\left(\sin\beta\cos\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right), \sin\beta\sin\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right),-\cos\beta\right)$$

Thus $|f_*(u)|=1$ by the trig identity $\sin^2\phi+\cos^2\phi=1$.

Intuitively $f_*(v)$ is horizontal, hence orthogonal to $f_*(u)$ the vector of steepest descent. Also $|f_*(v)|$ should be $|v|(=1)$ multiplied by $\frac{2\pi}{2\pi-\alpha}$ (as we scale up how fast we go round) multiplied by $\sin \beta=\frac{2\pi-\alpha}{2\pi}$ as the radius of the circle we go round is scaled down. Thus $|f_*(v)|=1$ and $f$ preserves orthonormal basis' of tangent spaces, hence is an isometry.

To confirm our intuition: $$f_*(v)=\frac1r\frac{\partial f}{\partial \theta}= \left(-\sin\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right), \cos\left( \theta \left(\frac{2\pi}{2\pi-\alpha}\right)\right),0\right)$$

This is clearly a unit vector and orthogonal to $f_*(u)$.

Answer 6

As a variant, avoiding the non-smoothness of the vertex of the cone:

Cut off a smaller cone from the top of the original cone. The resulting shape has a boundary, but no non-smooth points.

In greater generality, "singularities" can often be "excised", by removing a tubular neighborhood of them, but that does not produce a smooth boundary-less manifold.