3

I came up with the following problem: Given are two lines $g$ and $h$ and two points $P$ and $Q$. I'm looking for a geometric construction (using straightedge and compass) to find the line of reflection $l$ such that $P$ lies on $g'$ and $Q$ lies on $h'$. This seems easy but I cannot find the correct construction.

Below is an example with solution (using trial and error). Task Solution

garondal
  • 1,254
  • 3
    The lines-of-reflection that move $P$ onto $g$ (and $g$ onto $P$) are the tangents to the parabola with focus $P$ and directrix $g$; likewise for $Q$ and $h$. So, your question is effectively equivalent to finding a common tangent to two given parabolas. That doesn't necessarily make the problem easier, but seeing this interpretation might help spark ideas. (For visualization and experimentation, one can use GeoGebra's "tangents" command to draw the tangents common to two parabolas.) Note: By this question there are at most three such tangents. – Blue Jan 23 '25 at 23:52
  • Interesting way of looking at the problem. So it is probably not such a simple problem. Before I solved the problem of finding the point of reflection $l$ such that $P$ lies on $′$ and $$ lies on $ℎ′$, which was very easy. I thought this problem would be similarly hard. – garondal Jan 24 '25 at 04:50
  • "So it is probably not such a simple problem." ... I haven't investigated enough to decide whether "finding a reflecting line" is unexpectedly tricky for being equivalent to "finding a common tangent", or whether "finding a common tangent" is unexpectedly easy for being equivalent to merely "finding a reflecting a line". :) – Blue Jan 24 '25 at 05:06
  • Such a line may not exist. Are you asking to construct it when one exists? – Pranay Jan 24 '25 at 08:42
  • 1
    Yes (my above example there exists at least two solutions). Actually it would be enough if I get a construction for my example. – garondal Jan 24 '25 at 09:44
  • 1
    BTW: I'm now leaning toward the problem being unexpectedly tricky. Given that there are as many as three solutions, we're looking in general at solving a cubic equation somewhere, but arbitrary cube roots fall outside the realm of straightedge-and-compass constructibility. – Blue Jan 24 '25 at 23:48
  • So maybe there does not (always) exist a straightedge-and-compass construction? – garondal Jan 25 '25 at 10:58
  • @blue: https://math.stackexchange.com/questions/838182/given-a-pair-of-conics-construct-synthetically-their-shared-tangent-lines <- Here is a construction using basic geometry. – garondal Jan 28 '25 at 23:06

1 Answers1

1

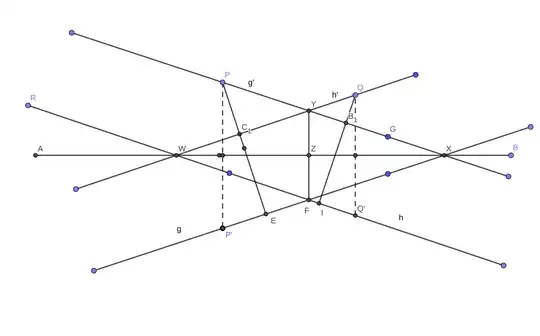
enter image description here

As can be seen in picture:

1- Drop perpendicular PE from P to line g.

2- Drop perpendicular QI from Q to line h.

3- Drop perpendicular $PB_1$ from P to segment QI, its extension intersects g at X.

4- Drop perpendicular $QC_1$ from P on segment PE, its extension intersects h at W.

We show that line WX is the reflect line; we have:

$PX||WI$ because they are both perpendicular on QI.

$QW||XE$ because they are both perpendicular on PE.

So quadrilateral WYXF is a rhombus and we have:

$\angle YWZ =\angle FWZ$

that is WY or h' is the reflection of h over WX and passes through points Q. Similarly :

$\angle YXZ =\angle FXZ$

which means YX or g' is the reflection of g over WX and passes through point P.

Note: may be this is a particular case. I could not show Z is mid point of WZ or YZ is the perpendicular bisector of WX. This is necessary fo WYXF to be a rhombus.

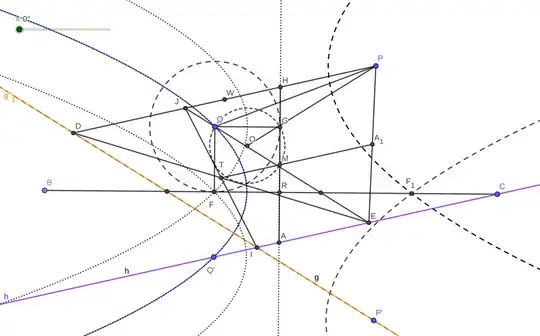
Update: I could construct this as can be seen in picture below:

1- QE is parallel with g.

2- PD is parallel with h.

3- T is where diagonals JI and DE intersect.

4-$A_1$ is the mid point of PE and intersects JE at M.

5- Circle O in constructed on diameter QM, it intersects PO at G.

The projection line BC is parallel with QG and have equal distance from Q to QE. You can find Q' and P' either by reflection over BC or drawing parabola with directrix MG and focus Q and P. The focii of the reflection of these parabola are the reflection of Q and P respectively.

Note : try this method and see whether it works or not.

enter image description here

sirous
  • 12,694
  • 1
    WYXF is a parallelogram, so its diagonals intersect at their midpoints, which means Z is a midpoint of both diagonals. But this doesn’t mean WYXF is a rhombus. – Pranay Jan 24 '25 at 18:26
  • 3
    You basically drew the line $g’$ through $Q$ parallel to $h$, and the line $h’$ through $P$ parallel to $g$, and looked at the line through points of intersection of $(g,g’)$ and $(h,h’)$. I don’t think this works in general except when $d(P,h)=d(Q,g)$. – Pranay Jan 24 '25 at 18:39
  • @Pranay, You are right, so it is a particular case. – sirous Jan 24 '25 at 20:25
  • What do you mean with "The projection line BC is parallel with QG and have equal distance from Q to QE."? – garondal Jan 25 '25 at 20:53