Based on this answer to my related Math StackExchange question, I believe the inverse Fourier transform of
$$F(\omega)=\text{csch}^2(\omega){\tag{1}}$$
is
$$f(t)=\mathcal{F}_{\omega}^{-1}[F(\omega)](t)=\int\limits_{-\infty}^{\infty} \text{csch}^2(\omega)\, e^{-2 i \pi \omega t} \, dt=-2 \pi^2 t \coth\left(\pi^2 t\right)\tag{2}$$
where the divergent integral in formula (2) above is evaluated using Hadamard regularization.
Assuming the Fourier inversion theorem holds, I believe $f(t)$ defined in formula (2) above can be recovered from $F(\omega)$ defined in formula (1) above via the nested Fourier series representation
$$f(x)=\lim_{N, f\to\infty}\left(\sum\limits_{n=1}^N \frac{\mu(2 n-1)}{2 n-1} \left(\sum\limits_{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k}{2 n-1}\right)\, F\left(\frac{k}{4 n-2}\right)\, \cos\left(\frac{\pi k x}{2 n-1}\right)\\-\frac{1}{4} \sum\limits_{k=1}^{4 f (2 n-1)} (-1)^k\, F\left(\frac{k}{8 n-4}\right)\, \cos\left(\frac{\pi k x}{4 n-2}\right)\right)\right)\tag{3}$$
where $\mu(n)$ is the Möbius function and the parameter $f$ in the upper evaluation limits of the two inner sums over $k$ is assumed to be a positive integer.
Formula (3) above is based on formula (11) in my question on a conjectured Fourier inversion theorem which I originally posted to Math StackExchange here and later cross-posted to Math Overflow here.
Question: Is formula (3) above a valid method of evaluating the divergent integral in formula (2) above using Hadamard regularization?
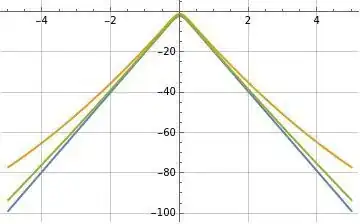
Figure (1) below illustrates $f(t)$ recovered from $F(\omega)$ using formula (3) above overlaid on the blue reference function $f(t)$ defined in formula (2) above where formula (3) is evaluated using the evaluation limits $N=10$ in orange and $N=40$ in green and where the evaluation limit $f=4$ is used in conjunction with both values of $N$. Note the evaluation of formula (3) more closely approximates $f(t)$ (blue) as the evaluation limit increases from $N=10$ (orange) to $N=40$ (green).
Figure (1): Illustration of $f(t)$ recovered from $F(\omega)$ using formula (3) (orange and green) overlaid on the blue reference function $f(t)$
The table below illustrates $f(4)$ recovered from $F(\omega)$ via formula (3) using several different values of the evaluation limits $N$ and $f$ where $f(4)\approx -78.9568$. Note the evaluation of formula (3) more closely approximates $f(4)$ as the evaluation limit $N$ increases, but seems to be less sensitive to the evaluation limit $f$.
$$\begin{array}{ccc} N & f & f(4) \\ \text{} & \text{} & \text{} \\ 10 & 4 & -64.6768 \\ 10 & 8 & -64.6769 \\ 10 & 16 & -64.6769 \\ \text{} & \text{} & \text{} \\ 20 & 4 & -65.3333 \\ 20 & 8 & -65.3333 \\ 20 & 16 & -65.3333 \\ \text{} & \text{} & \text{} \\ 40 & 4 & -75.3896 \\ 40 & 8 & -75.3897 \\ 40 & 16 & -75.3897 \\ \text{} & \text{} & \text{} \\ 80 & 4 & -75.5236 \\ 80 & 8 & -75.5236 \\ 80 & 16 & -75.5236 \\ \text{} & \text{} & \text{} \\ 160 & 4 & -78.1308 \\ 160 & 8 & -78.1308 \\ 160 & 16 & -78.1308 \\ \end{array}$$
The table below illustrates $f(0)$ recovered from $F(\omega)$ via formula (3) using several different values of the evaluation limits $N$ and $f$ where $f(0)=\underset{t\to 0}{\text{lim}}f(t)=-2$. Note the evaluation of formula (3) more closely approximates $f(0)$ as the evaluation limit $N$ increases, but seems to be less sensitive to the evaluation limit $f$.
$$\begin{array}{ccc} N & f & f(0) \\ \text{} & \text{} & \text{} \\ 10 & 4 & -0.889998 \\ 10 & 8 & -0.888711 \\ 10 & 16 & -0.888711 \\ \text{} & \text{} & \text{} \\ 20 & 4 & -0.941088 \\ 20 & 8 & -0.939799 \\ 20 & 16 & -0.939799 \\ \text{} & \text{} & \text{} \\ 40 & 4 & -1.72372 \\ 40 & 8 & -1.7224 \\ 40 & 16 & -1.7224 \\ \text{} & \text{} & \text{} \\ 80 & 4 & -1.73415 \\ 80 & 8 & -1.73282 \\ 80 & 16 & -1.73282 \\ \text{} & \text{} & \text{} \\ 160 & 4 & -1.93705 \\ 160 & 8 & -1.93572 \\ 160 & 16 & -1.93572 \\ \end{array}$$