What is the Fourier transform of $\text{csch}^2(t)$?

Question

Mathematica indicates the Fourier transform of $\text{csch}^2(t)$ is

$$\mathcal{F}_t\left[\text{csch}^2(t)\right](\omega)=-\frac{\pi \omega \coth\left(\frac{\pi \omega}{2}\right)+2}{\sqrt{2 \pi}}\tag{1}$$

but also indicates

$$\mathcal{F}_{\omega }^{-1}\left[-\frac{\pi \omega \coth\left(\frac{\pi \omega}{2}\right)+2}{\sqrt{2 \pi}}\right](t)=\text{csch}^2(t)-2\, \delta(t)\tag{2}$$

and

$$\mathcal{F}_{\omega}^{-1}\left[-\frac{\pi \omega \coth \left(\frac{\pi \omega}{2}\right)}{\sqrt{2 \pi }}\right](t)=\text{csch}^2(t)\tag{3}$$

but I'm wondering if

$$\mathcal{F}_t\left[\text{csch}^2(t)\right](\omega)=-\frac{\pi \omega \coth\left(\frac{\pi \omega}{2}\right)}{\sqrt{2 \pi}}\tag{4}$$

implied by the evaluation in formula (3) above is even correct.

---

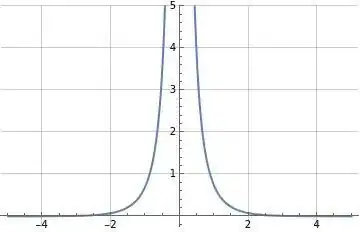
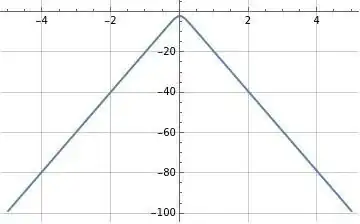
Figures (1) and (2) below illustrate $\text{csch}^2(t)$ and $-\frac{\pi \omega \coth\left(\frac{\pi \omega}{2}\right)}{\sqrt{2 \pi}}$ which is the conjectured result illustrated in formula (4) above.

---

Figure (1): Illustration of $\text{csch}^2(t)$

---

Figure (2): Illustration of $-\frac{\pi \omega \coth\left(\frac{\pi \omega}{2}\right)}{\sqrt{2 \pi}}$

---

I'm wondering if the result in formula (4) above should really be

$$\mathcal{F}_t\left[\text{csch}^2(t)\right](\omega )=\left\{\begin{array}{cc} -\frac{\pi \omega \coth \left(\frac{\pi \omega}{2}\right)}{\sqrt{2 \pi }} & -\omega_0<\omega <\omega_0 \\ 0 & \text{otherwise} \\ \end{array}\right.\tag{5}$$

for some $\omega_0>0$, or perhaps the inverse Fourier transform illustrated in formula (3) above only converges in a distributional sense?

---

Update:

---

After exploring this question and this answer posted below a bit more I'm beginning to suspect the result illustrated in formula (4) above is correct.

---

The evaluations above assumed the Fourier and inverse Fourier transforms are defined as

$$F(\omega)=\mathcal{F}_t[f(t)](\omega)=\frac{1}{\sqrt{2 \pi}} \int\limits_{-\infty}^{\infty} f(t)\, e^{i \omega t} \, dt\tag{6}$$

and

$$f(t)=\mathcal{F}_{\omega}^{-1}[F(\omega)](t)=\frac{1}{\sqrt{2 \pi}} \int\limits_{-\infty}^{\infty} F(\omega)\, e^{-i t \omega} \, d\omega\tag{7}$$

respectively.

---

I believe this answer posted below assumes the Fourier and inverse Fourier transforms are defined as

$$\mathcal{F}_t[f(t)](\omega)=\int_{-\infty}^{\infty} f(t)\, e^{i \omega t} \, dt\tag{8}$$

and

$$\mathcal{F}_{\omega}^{-1}[F(\omega)](t)=\frac{1}{2 \pi} \int\limits_{-\infty}^{\infty} F(\omega)\, e^{-i t \omega} \, d\omega\tag{9}$$

respectively.

---

Formulas (8) and (9) above can be evaluated as

$$\mathcal{F}_t[f(t)](\omega)=2 \int_0^{\infty} f(t)\, \cos(\omega t) \, dt\tag{10}$$

and

$$\mathcal{F}_{\omega}^{-1}[F(\omega)](t)=\frac{1}{\pi} \int\limits_0^{\infty} F(\omega)\, \cos(t \omega) \, d\omega\tag{11}$$

respectively when $f(t)$ and $F(\omega)$ are even functions of $t$ and $\omega$ respectively.

---

I believe the definitions in formulas (8) and (10) above lead to

$$\mathcal{F}_t\left[\text{csch}^2(t)\right](\omega)=-\pi \omega\, \coth \left(\frac{\pi \omega }{2}\right)\tag{12}$$

and using the definition in Formula (8) above Mathematica indicates

$$\mathcal{F}_t\left[\frac{1}{t^2}\right](\omega)=\int_{-\infty}^{\infty} \frac{1}{t^2}\, e^{i \omega t} \, dt=-\pi \omega\, \text{sgn}(\omega)\tag{13}$$

which is consistent with

$$\mathrm{FP} \int\limits_{-\infty}^{\infty} \frac{1}{t^2} \, dt=0\tag{14}$$

in this answer posted below.

---

Answer 1

$\DeclareMathOperator{\csch}{csch}$ $\newcommand{\abs}[1]{\left\lvert #1 \right\rvert}$ $\newcommand{\d}{\mathrm{d}}$ $\newcommand{\e}{\mathrm{e}}$

As $\csch^2 t$ is even, let's work with cosine transforms. To begin with, consider the genuinely convergent integrals $$\begin{align}\int_{-\infty}^{\infty} \left(\frac{\tau^2}{t^2}-\pi^2\csch^2\frac{\pi t}{\tau}\right) \cos \omega t \frac{\d t}{2\pi\abs{\tau}} &= \frac{\abs{\omega \tau}}{\e^{\abs{\omega \tau}}-1}\\ \int_{-\infty}^{\infty}\frac{\tau^2}{t^2}(1-\cos\omega t)\frac{\d t}{2\pi \abs{\tau}}&=\tfrac{1}{2}\abs{\omega \tau}\end{align}$$ (cf. Bateman's Tables of Integral Transforms, eqs. 1.4.8 and 6.5.15). Adding gives us another convergent integral $$\begin{split}\int_{-\infty}^{\infty} \left(\frac{\tau^2}{t^2}-\pi^2\csch^2\frac{\pi t}{\tau} \cos \omega t\right) \frac{\d t}{2\pi\abs{\tau}}&=\tfrac{1}{2}\abs{\omega \tau}+\frac{\abs{\omega \tau}}{\e^{\abs{\omega \tau}}-1}\\&=\frac{\omega\tau}{2}\coth\frac{\omega\tau}{2}\text{.}\end{split}$$ As whatever notion of generalized integration we choose ought to be a linear functional, the ambiguity in defining the transform of $\csch^2 t$ reduces to deciding what the interpretation of $\int_{-\infty}^{\infty} \frac{\d t}{t^2}$ is supposed to be. The choice of the Hadamard finite part integral entails $$\mathrm{FP}\int_{-\infty}^{\infty}\frac{\d t}{t^2} = 0$$ so that $$\mathrm{FP}\int_{-\infty}^{\infty}\left(\frac{\tau^2}{t^2}\right)\cos\omega t \frac{\d t}{2\pi \abs{\tau}}=-\tfrac{1}{2}\abs{\omega\tau}$$ and $$\boxed{\mathrm{FP}\int_{-\infty}^{\infty} \left(\pi^2\csch^2\frac{\pi t}{\tau}\right) \cos \omega t \frac{\d t}{2\pi\abs{\tau}} =-\frac{\omega\tau}{2}\coth\frac{\omega\tau}{2}}\text{.}$$

---

Another potential starting point is the (genuine) integral $$\int_{-\infty}^{\infty} \left(\pi^2\csch^2\frac{\pi t}{\tau}\right) (1-\cos \omega t) \frac{\d t}{2\pi\abs{\tau}} =\frac{\omega\tau}{2}\coth\frac{\omega\tau}{2}-1\text{.}$$ Then interpreting $\int \pi^2\csch^2\frac{\pi t}{\tau}\cos \omega t\frac{\d t}{2\pi\abs{\tau}}$ boils down to deciding what interpretation we should give to$\int \pi^2\csch^2\frac{\pi t}{\tau}\frac{\d t}{2\pi\abs{\tau}}$.