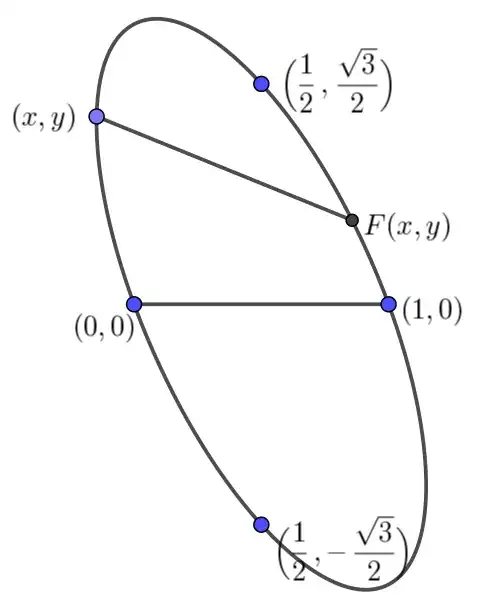
Define $F(x,y)$ to be the triangle center X(1138) of the triangle $\{(0,0),(1,0),(x,y)\}$.
$$ F(x,y)=\left(\tiny\begin{aligned} \frac{(12 x - 21 x^2 + 6 x^3 + 3 x^4 - 5 y^2 - 2 x y^2 + 6 x^2 y^2 + 3 y^4) (9 x^3 - 18 x^4 + 9 x^5 + 9 x y^2 - 30 x^2 y^2 + 18 x^3 y^2 - 4 y^4 + 9 x y^4)}{3 ((y-2 x y)^2+(3 x^2-3 x+y^2)^2)^2},\\ \frac{(-9 x^2 + 27 x^3 - 27 x^4 + 9 x^5 + 3 y^2 + 3 x y^2 - 24 x^2 y^2 + 18 x^3 y^2 - 5 y^4 + 9 x y^4) (9 x^3 - 18 x^4 + 9 x^5 + 9 x y^2 - 30 x^2 y^2 + 18 x^3 y^2 - 4 y^4 + 9 x y^4)}{3 y ((y-2 x y)^2+(3 x^2-3 x+y^2)^2)^2} \end{aligned}\right) $$ $F$ is an involution ($F$ interchanges pairs of points) $F\circ F=\text{id}$, by this thread.
$F$ has four singularities: $(0,0),(1,0),(\frac12,\pm\frac{\sqrt3}2)$.
The question is to find the curves $S$ such that $F(S)\subseteq S$.
Example 1
If $(x,y)$ is on the line $x=\frac12$, then $F(x,y)$ stays on the line $x=\frac12$ by symmetry.
So the line $x=\frac12$ satisfies the condition.
Moreover, if $S$ satisfies the condition then so does the reflection of $S$ across $x=\frac12$.
Example 2
$F$ has infinitely many fixed points. Simplifying $F(x,y)=(x,y)$ we get a curve $$3 y^6-\left(3 x^2-3 x+5\right) y^4-3 (x-1) x \left(5 x^2-5 x+3\right) y^2-9 (x-1)^3 x^3=0$$ through the four singularities of $F$.
Example 3
$F(x,\sqrt3x)=(1+x,\sqrt3x)$, so the pair of parallel lines joining the four singularities of $F$ $$(y-\sqrt3x)(y-\sqrt3(x-1))=0\label1\tag1$$satisfies the condition.
Reflecting across $x=\frac12$, we get the other pair of parallel lines joining the four singularities of $F$ $$(y+\sqrt3x)(y+\sqrt3(x-1))=0\label2\tag2$$ also satisfies the condition.
To generalize Example 3, consider the pencil of conics through four singularities of $F$ $${\cal C}:\quad\eqref{1}-\mu\eqref{2}$$ for a constant $\mu\in\mathbb{P}^1$.
The center of $\cal C$ is $(\frac12,0)$.
(I) The point $F(x,y)\in\cal C$ for all point $(x,y)\in\cal C$.
(II) The slope of the line through $(x,y)$ and $F(x,y)$ is the same for all points $(x,y)\in\cal C$.
So the restriction of $F$ to $\cal C$ is a projective transformation.
(III) $\cal C$ is the locus of the point $P$ such that the Euler line of the triangle $\{(0,0),(1,0),P\}$ is parallel to the Euler line of the triangle $\{(0,0),(1,0),(x,y)\}$.
In particular, the intersection of the line through $(x,y)$ parallel to the Euler line of the triangle $\{(0,0),(1,0),(x,y)\}$ and the circumcircle lies on $\cal C$.
To prove (I) is equivalent to prove that $$\mu(x,y)=\mu(F(x,y))\tag3\label3$$ where $ \mu(x,y)=\frac{(y-\sqrt3x)(y-\sqrt3(x-1))}{(y+\sqrt3x)(y+\sqrt3(x-1))} $ is the constant that determines $\cal C$.
Plugging the long expression of $F(x,y)$ into \eqref{3} proves (I).
How do you prove (II) and (III)? I tried hard, but I was lost in the computation.
The above are examples of curves $S$ such that $F(S)\subseteq S$
Are there any other $S$?