Suppose $A$ is a $d\times d$ matrix formed by multiplying $d$ random matrices of the form $I-vv^T$ where $v$ is sampled isotropically from the unit sphere.
It appears that various various values of $d$, $\operatorname{Tr}(A)$ and $\|A\|_F^2$ are almost equal, how can we explain this fact?
Background:
It is easy to show that the $\operatorname{tr}(A)$ and $\|A\|_F^2=\operatorname{tr}(A'A)$ have the same mean $d(1-\frac{1}{d})^d$. The hard part, which I am not able to answer here, is whether (or why) the distributions of $\operatorname{tr}(A)$ and $\|A\|_F^2$ are highly concentrated about their common mean.
Let $P_i=I-v_iv_i'$ where $v_1,v_2,\ldots,v_d$ be independently and uniformly sampled from the unit sphere. Consider any matrix product of the form $P_{j_1}P_{j_2}\cdots P_{j_k}$. For every constant unitary matrix $Q$, since $Qv_1$ has the same distribution as $v_i$, we have $$ E(P_{j_1}P_{j_2}\cdots P_{j_k}) =E\left((QP_{j_1}Q')(QP_{j_2}Q')\cdots (Q'P_{j_k}Q)\right) =QE(P_{j_1}P_{j_2}\cdots P_{j_k})Q'. $$ That is, $E(P_{j_1}P_{j_2}\cdots P_{j_k})$ is invariant under every unitary similarity transform. Hence it must be a scalar multiple of $I$.
In particular, as $E(P_i)=E(I-v_iv_i')$ has trace $d-1$, it must be equal to $cI$ where $c=1-\frac{1}{d}$. Hence \begin{align*} E(A) &=E\left(P_1P_2\cdots P_d\right)\\ &=E(P_1)E(P_2)\cdots E(P_d)\\ &=c^dI,\\ E\left(AA'\right) &=E\left(P_1P_2\cdots P_{d-1}P_dP_dP_{d-1}\cdots P_1\right)\\ &=E\left(P_1P_2\cdots P_{d-1}P_dP_{d-1}\cdots P_1\right)\\ &=E\left(P_1P_2\cdots P_{d-1}E(P_d)P_{d-1}\cdots P_1\right)\\ &=E\left(P_1P_2\cdots P_{d-1}(cI)P_{d-1}\cdots P_2P_1\right)\\ &=cE\left(P_1P_2\cdots P_{d-1}P_{d-1}\cdots P_2P_1\right)\\ &=\cdots\\ &=c^dE(I)=c^dI. \end{align*} It follows that $E(\operatorname{tr}(A))=dc^d=E(\operatorname{tr}(AA'))=E(\|A\|_F^2)$
We can abstract each update as $$B = (I - vv^T) A,\tag{*}$$ where $v$ is chosen from the unit hypersphere independent of the choices of $A$. Our derivation will use the following facts: $$ \begin{align} \mathbb{E}[vv^T] = \frac{1}{d} \cdot I, \qquad \mathbb{E}[(v^TMv)^2] = \frac{1}{d(d+2)} \left[\operatorname{tr}^2(M) + \operatorname{tr}(M^TM)+ \operatorname{tr}(M^2)\right] \end{align}. $$
From (*) we get $$ \begin{align} \operatorname{tr}(B) &= \operatorname{tr}(A) - v^TAv \end{align} $$ and $$\operatorname{tr}^2(B) = \operatorname{tr}^2(A) - 2 \operatorname{tr}(A) \cdot v^TAv + (v^TAv)^2.$$
Taking the conditional expectation, we have $$ \mathbb{E}[\operatorname{tr}^2(B)|A] = \left(1-\frac{2}{d}\right)\operatorname{tr}^2(A) + \frac{1}{d(d+2)}\left[\operatorname{tr}^2(A) + \operatorname{tr}(A^TA)+ \operatorname{tr}(A^2)\right].\tag{1} $$ Similarly, as $B^2 = (I - vv^T) A(I - vv^T) A = A^2 - vv^T A^2 - Avv^TA + vv^TAvv^TA$, we have $$\operatorname{tr}(B^2) = \operatorname{tr}(A^2) - 2v^TA^2v + (v^TAv)^2$$ and $$\mathbb{E}[\operatorname{tr}(B^2)|A] = \left(1-\frac{2}{d}\right)\operatorname{tr}(A^2) + \frac{1}{d(d+2)} \left[\operatorname{tr}^2(A) + \operatorname{tr}(A^TA)+ \operatorname{tr}(A^2)\right].\tag{2}$$ Also, since $B^TB = A^T(I-vv^T)A = A^TA - A^Tvv^TA$, we have $$\mathbb{E}[\operatorname{tr}(B^TB)|A] = \left(1-\frac{1}{d}\right) \operatorname{tr}(A^TA) .\tag{3}$$
Taking another expectation of (1)-(3), we get $$ \begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(B)]\\ \mathbb{E}[\operatorname{tr}(B^2)]\\ \mathbb{E}[\operatorname{tr}(B^TB)] \end{bmatrix} = C \begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(A)]\\ \mathbb{E}[\operatorname{tr}(A^2)]\\ \mathbb{E}[\operatorname{tr}(A^TA)] \end{bmatrix},\qquad C = \begin{bmatrix} 1-\frac{2}{d} + \frac{1}{d(d+2)} & \frac{1}{d(d+2)} & \frac{1}{d(d+2)}\\ \frac{1}{d(d+2)} & 1-\frac{2}{d} + \frac{1}{d(d+2)} & \frac{1}{d(d+2)}\\ 0 & 0 & 1-\frac{1}{d} \end{bmatrix}. $$
The matrix $C$ has eigenvalues $\lambda_1 = 1-\frac{2}{d}+ \frac{2}{d(d+2)}, \lambda_2 = 1-\frac{2}{d}, \lambda_3 = 1-\frac{1}{d}$, with corresponding eigenvectors $(1, 1, 0)^T, (1, -1, 0)^T, (1, 1, d)^T$.
The initial condition is $A = I$, and $\begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(A)]\\ \mathbb{E}[\operatorname{tr}(A^2)]\\ \mathbb{E}[\operatorname{tr}(A^TA)] \end{bmatrix} = \begin{bmatrix}d^2\\ d\\ d\end{bmatrix} = \frac{d^2 + d - 2}{2} \begin{bmatrix} 1 \\ 1 \\ 0\end{bmatrix} + \frac{d^2 - d}{2} \begin{bmatrix} 1 \\ -1 \\ 0\end{bmatrix} + \begin{bmatrix} 1 \\ 1 \\ d\end{bmatrix} $.
Therefore, after iterating $d$-steps, we obtain the result $$\begin{align} \mathbb{E}[\operatorname{tr}^2(A)] &= \frac{d^2 + d - 2}{2} \cdot \lambda_1^d + \frac{d^2 - d}{2} \cdot \lambda_2^d + \lambda_3^d\\ &= \frac{d^2 + d - 2}{2} \cdot \left(1-\frac{2}{d}+ \frac{2}{d(d+2)}\right)^d + \frac{d^2 - d}{2} \cdot \left(1-\frac{2}{d}\right)^d + \left(1-\frac{1}{d}\right)^d.\end{align} $$ As $\mathbb{E}[\operatorname{tr}(A)] = \left(1-\frac{1}{d}\right)^d d$, we have $$ \begin{align} \operatorname{var}(\operatorname{tr}(A)) &= \mathbb{E}[\operatorname{tr}^2(A)] - (\mathbb{E}[\operatorname{tr}(A)])^2 \\ &= \frac{d^2 + d - 2}{2} \cdot \left(1-\frac{2}{d}+ \frac{2}{d(d+2)}\right)^d + \frac{d^2 - d}{2} \cdot \left(1-\frac{2}{d}\right)^d + \left(1-\frac{1}{d}\right)^d - \left(1-\frac{1}{d}\right)^{2d} d^2. 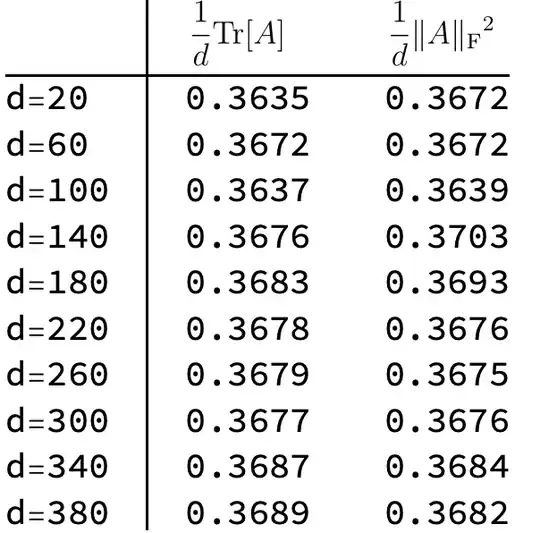\end{align} $$ which has a constant limit $\frac{-3 + 2 e}{2 e^2}$from Wolfram Alpha.
Remarks:
$$ \begin{align}\mathbb{E}[\operatorname{tr}(A^2)] &= \frac{d^2 + d - 2}{2} \left(1-\frac{2}{d}+ \frac{2}{d(d+2)}\right)^d - \frac{d^2 - d}{2}\left(1-\frac{2}{d}\right)^d + \left(1-\frac{1}{d}\right)^d\\ &= \frac{2d}{e^2} + \frac{e - 3}{e^2} + O\left(\frac1d\right) \end{align} \tag{P1} $$ (asymptotic from Wolfram Alpha)
On $\operatorname{var}(\operatorname{tr}(A^TA))$:
Since $$B^TB = A^T(I-vv^T)A = A^TA - A^Tvv^TA,\tag{#}$$ we have $ \operatorname{tr}(B^TB) = \operatorname{tr}(A^TA) - v^TAA^Tv$, and $\operatorname{tr}^2(B^TB) = \operatorname{tr}^2(A^TA) - 2 \operatorname{tr}(A^TA) \cdot v^TAA^Tv + (v^TAA^Tv)^2. $ Therefore,
$$ \mathbb{E}[\operatorname{tr}^2(B^TB)|A] = \left(1 - \frac{2}{d}\right)\operatorname{tr}^2(A^TA) + \frac{1}{d(d+2)} \left[\operatorname{tr}^2(A^TA) + 2\operatorname{tr}((A^TA)^2)\right]. $$
Similarly, from (#), we obtain $$\begin{align}(B^TB)^2 &= (A^TA - A^Tvv^TA)(A^TA - A^Tvv^TA) \\ &= (A^TA)^2 - A^TAA^Tvv^TA - A^Tvv^TAA^TA + (A^Tvv^TA)^2 \end{align}$$ and thus
$$\mathbb{E}[\operatorname{tr}((B^TB)^2)|A] = \left(1 - \frac{2}{d}\right)\operatorname{tr}((A^TA)^2) + \frac{1}{d(d+2)} \left[\operatorname{tr}^2(A^TA) + 2\operatorname{tr}((A^TA)^2)\right]. $$
Taking another expectation, we obtain
$$ \begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(B^TB)]\\ \mathbb{E}[\operatorname{tr}((B^TB)^2)] \end{bmatrix} = C' \begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(A^TA)]\\ \mathbb{E}[\operatorname{tr}((A^TA)^2)] \end{bmatrix},\qquad C' = \begin{bmatrix} 1-\frac{2}{d} + \frac{1}{d(d+2)} & \frac{2}{d(d+2)} \\ \frac{1}{d(d+2)} & 1-\frac{2}{d} + \frac{2}{d(d+2)} \end{bmatrix}. $$
The matrix $C'$ has eigenvalues $\lambda_1 = 1-\frac{2}{d} + \frac{3}{d(d+2)}, \lambda_2 = 1-\frac{2}{d}$, and corresponding eigenvectors $(1, 1)^T$ and $(2, -1)^T$.
The initial condition is $ A = I$ and $\begin{bmatrix} \mathbb{E}[\operatorname{tr}^2(A^TA)]\\ \mathbb{E}[\operatorname{tr}((A^TA)^2)] \end{bmatrix} = \begin{bmatrix} d^2\\d \end{bmatrix} = \frac{d^2+2d}{3} \begin{bmatrix} 1\\1\end{bmatrix} + \frac{d^2-d}{3} \begin{bmatrix} 2\\-1\end{bmatrix} $.
Therefore, after iterating $d$-steps, we obtain the result $$\begin{align} \mathbb{E}[\operatorname{tr}^2(A^TA)] &= \frac{d^2+2d}{3} \left(1-\frac{2}{d} + \frac{3}{d(d+2)}\right)^d + 2 \cdot \frac{d^2-d}{3} \left(1-\frac{2}{d}\right)^d .\end{align} $$ As $\mathbb{E}[\operatorname{tr}(A^TA)] = \left(1-\frac{1}{d}\right)^d d$, we have $$ \begin{align} \operatorname{var}(\operatorname{tr}(A^TA)) &= \mathbb{E}[\operatorname{tr}^2(A^TA)] - (\mathbb{E}[\operatorname{tr}(A^TA)])^2 \\ &= \frac{d^2+2d}{3} \left(1-\frac{2}{d} + \frac{3}{d(d+2)}\right)^d + 2 \cdot \frac{d^2-d}{3} \left(1-\frac{2}{d}\right)^d - \left(1-\frac{1}{d}\right)^{2d} d^2. \end{align} $$ which has a constant limit $1/e^2$ from Wolfram Alpha.
We also get $$ \begin{align} \mathbb{E}[\operatorname{tr}((A^TA)^2)] &= \frac{d^2+2d}{3} \left(1-\frac{2}{d} + \frac{3}{d(d+2)}\right)^d - \frac{d^2-d}{3} \left(1-\frac{2}{d}\right)^d\\ &= \frac{2d}{e^2} -\frac{1}{2e^2} + O\left(\frac1d\right) ,\end{align}\tag{P2} $$ (asymptotic from Wolfram Alpha)
We can compare (P2) with (P1) and show their expectations have the same linear term. This is related to the case $p = 2$ discussed in this post "Why is $\operatorname{Tr}(A^p)\approx \sum_i \sigma_i^{2p}$ for this random matrix?".
