4

I have a non-normal matrix $A$ with eigenvalues $\lambda_i$ and singular values $\sigma_i$. For integer $s>1$, empirically I observe the following:

$$\sum_i \lambda_i^s = \sum_i \sigma_i^{2s}$$

What does this tell me about my matrix $A$?

Here are observed values for a non-normal matrix $A_d$ described in this question with $d=1000$.

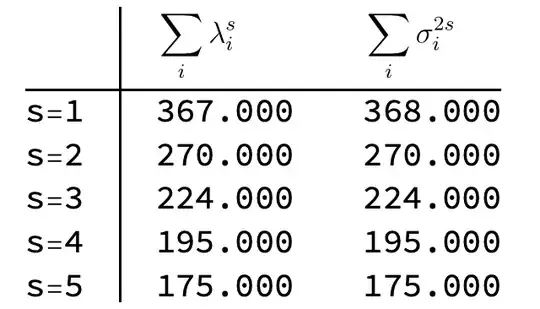
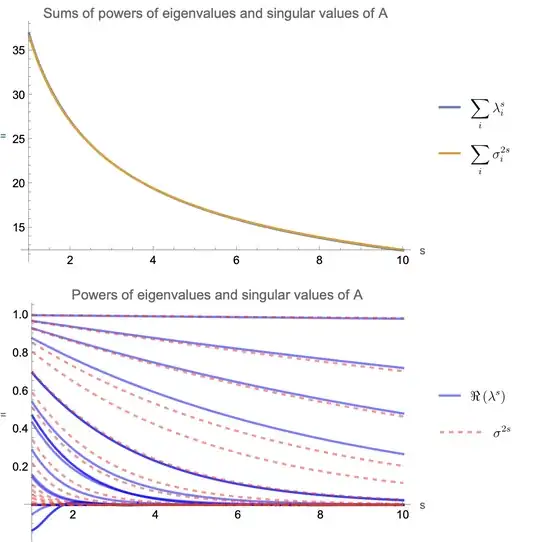
Here's what eigenvalues of the matrix in question look like for various values of $s$ enter image description here

You can see that squared singular values and real parts of eigenvalues are generally distinct, however their sums appear to stay the same

enter image description here

Notebook

Yaroslav Bulatov
  • 5,579

1 Answers1

1

Some quick observations. The given condition holds if and only if $A$ and $A^\ast A$ have the same characteristic polynomial, i.e., if and only if $\lambda_i(A)=\sigma_i(A)^2$ for each $i$ when the eigenvalues of $A$ are arranged in descending order.

In particular, $\rho(A)=\lambda_1(A)=\sigma_1(A)^2=\|A\|_2^2$. Since $\rho(A)\le\|A\|_2$ in general, we must have $\lambda_1(A)=\sigma_1(A)^2\le1$. Hence $A$ is unitarily similar to $\pmatrix{I\\ &B}$ for some matrix $B$ with $\lambda_i(B)=\sigma_i(B)^2$ for each $i$ and $\|B\|_2<1$. (Here $B$ is void and $A=I$ if $\|A\|_2=1$; $I$ is void and $B=A$ if $\|A\|_2<1$.) In particular, $\det(B)=\det(B^\ast B)$. Hence $\det(B)$ is either $0$ or $1$. Since $\|B\|_2<1$, $|\det(B)|<1$. Therefore $B$ must be singular if it is not empty.

$B$ can be quite arbitrary. E.g. suppose that we want $r=\operatorname{rank}(B)\le\dim\ker(B)$. Let $X$ be any $r\times r$ triangular matrix with all eigenvalues in $(0,1)$. When the off-diagonal entries of $X$ are sufficiently small, its singular values will be very close to its eigenvalues. Therefore $\sigma_i(X)^2<\lambda_i(X)$. Let $USV^\ast$ be a singular value decomposition of $X$. Let $D=\operatorname{diag}\left(\sqrt{\lambda_1(X)-\sigma_1(X)^2},\ldots,\sqrt{\lambda_r(X)-\sigma_r(X)^2}\right)$ and $$ B=\pmatrix{X&0&0\\ UDV^\ast&0_{r\times r}&0\\ 0&0&0}. $$ Then $\lambda_i(B)=\sigma_i(B)^2$ for each $i$, $\|B\|_2<1$ and $\det(B)=0$.

user1551
  • 149,263
  • The matrix in my example has complex-valued eigenvalues, so characteristic polynomials are different – Yaroslav Bulatov Dec 25 '24 at 19:05
  • @YaroslavBulatov Then in your case, the pattern cannot continue indefinitely. It must break down at some larger $s$. – user1551 Dec 25 '24 at 19:19
  • Interesting. I've tested it out for $s$ until $s=20$ and the correspondence still holds, I'm wondering how unexpected/unusual that is (the matrix is a product of random symmetric rank-1 projections) – Yaroslav Bulatov Dec 25 '24 at 19:43
  • 1
    @YaroslavBulatov But it is a well-known fact that if $X^s$ and $Y^s$ have the same trace for all $s$, then $X$ and $Y$ must have the same eigenvalues. This is a simple consequence of Newton identities. – user1551 Dec 25 '24 at 19:48
  • @YaroslavBulatov If $A_d$ is a product of some $k<<d$ projections, then what you observed is expected, because the $x_i$s tend to be mutually orthogonal in a space of very high dimensions. Yet your $A_d$ is a product of $d$ projections... this is a bit strange. – user1551 Dec 25 '24 at 19:52
  • yes, this is indeed strange, I've forked a simpler question of explaining why trace is equal to squared Frobenius norm here – Yaroslav Bulatov Dec 25 '24 at 20:22
  • Regarding the well-known fact about $X,Y$ having the same eigenvalues, is it the case for normal matrices only, or does it work for non-normal as well? In this case $A$ has eigenvalues appearing in conjugate pairs, meanwhile $AA^T$ has no such restriction, added plots – Yaroslav Bulatov Dec 26 '24 at 00:31
  • @YaroslavBulatov It holds for all square matrices, normal or non-normal. See https://math.stackexchange.com/q/88424 or https://math.stackexchange.com/q/597743 This is actually not a property of matrices, but a property of polynomials. Given two families of complex numbers $\lambda_1,\ldots,\lambda_d$ and $\mu_1,\ldots,\mu_d$, if $\sum_i\lambda_i^s=\sum_i\mu_i^s$ for every $s\in{1,2,\ldots,d}$, the two families must be identical, i.e., there exists a permutation $\sigma$ of ${1,2,\ldots,d}$ such that $\lambda_i=\mu_{\sigma(i)}$ for each $i$. – user1551 Dec 26 '24 at 07:46
  • Ah I see, so it could be just equality in probability. Intermediate question is why $E\operatorname{Tr}A^2\approx \sum_i \sigma_i^4$ – Yaroslav Bulatov Dec 26 '24 at 19:48