9

Wikipedia's entry on the subject gives the definition, "constructing a square with the area of a given circle [...] with a compass and straightedge", and immediately reports the well-known fact that "the task was proven to be impossible, as [...] $\pi$ is a transcendental number".

But it also dedicates a paragraph to approximate constructions, giving a great recap of the spirit of such findings: "Although squaring the circle exactly with compass and straightedge is impossible, approximations to squaring the circle can be given by constructing lengths close to $\pi$. It takes only elementary geometry to convert any given rational approximation of $\pi$ into a corresponding compass and straightedge construction, but such constructions tend to be very long-winded in comparison to the accuracy they achieve. After the exact problem was proven unsolvable, some mathematicians applied their ingenuity to finding approximations to squaring the circle that are particularly simple among other imaginable constructions that give similar precision."

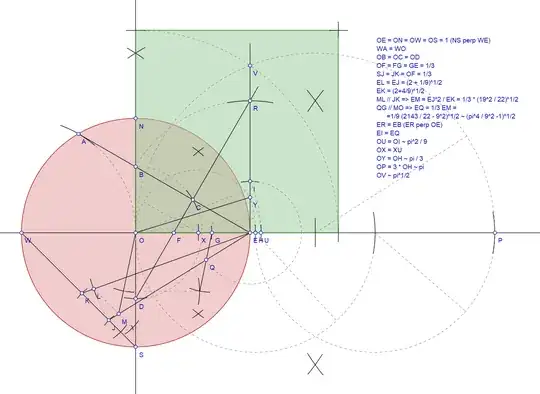
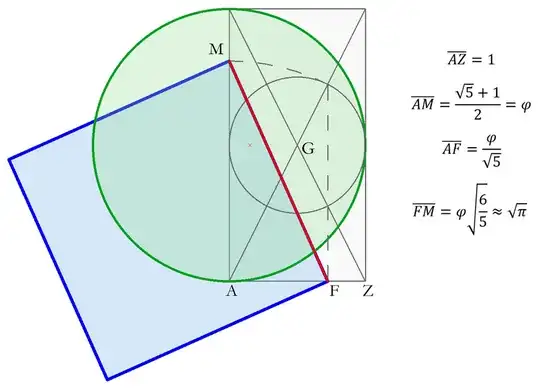
It proceeds to list some notable historical examples, culminating in Ramanujan's finding. Based on his own famous approximation for $\pi \approx \sqrt[4]{\frac{2143}{22}}$, which is indeed constructible, and thanks to a clever arrangement it results in a very elegant construction featuring an impressive precision: the side of the square is off by just above $0.02$ mm (or $\approx 1$ mil) when the circle's diameter is $150$ km ($\approx 100$ miles).

enter image description here

I was wondering whether Ramanujan's construction still stands today as the best one. In this context, of course, there is no objective definition of "best". In the spirit of the introduction, let's just say that the construction should yield the maximum possible precision while still being simple enough to be practical for hand-drawing.

So, my questions: are there today better constructions than Ramanujan's? If so, can you provide reference? Aren't they listed on Wikipedia (or anywhere else, as far as I can find) because they would just be uninsteresting today? Or is still, in fact, an exacting task to provide an improvement over Ramanujan's extraordinary finding? In case one was found today, would it be considered sensational/interesting/ordinary/insignificant?

Update: Tankut's answer brought up a $2019$ preprint by H.V. Chu. It was mentioned having in mind a different kind of "challenge", but in the same paper the author is also proposing a construction that should improve upon Ramanujan's under my terms. But that is exactly an example of what I'm ruling out: to me, despite his laudable efforts, and contrary to his claim, drawing it would still be impractical (in fact he doesn't, not fully). He also claims that his would be a record, apparently confirming that Ramanujan's is still the benchmark to beat. This encourages me on my path: I might have a lead toward a construction fulfilling the goal. I'm still keen to know how significant this would be according to the standards of modern mathematics!

lesath82
  • 2,605
  • I think this must be a matter of taste - how long are you willing to construct? The Kochanski and De Gelder constructs take about 10 or 15s to do each and give 4 and 6 decimal places accuracy. The Ramanujan construct is much longer, takes a minute or two to construct, but gives 8 places. I favor de Gelders as “best” balance of steps vs precision. – RobinSparrow Dec 23 '24 at 13:17
  • 1
    @RobinSparrow Yes, I also love de Gelder's construction, in fact I had my handmade version on my whiteboard for some time :-). But, aiming for the highest possible precision, is there any actual improvement over Ramanujan's which is still humanly possible to hand-draw without having the drawing become an absolute mess? I'd be willing to dive into matters of taste, if I were aware of alternatives... – lesath82 Dec 23 '24 at 13:35
  • Inefficient one comes to mind. You can approximate a circle with a polygon of arbitrarily many sides. Any polygon can be "squared". So one of problems with squaring the circle is doing it with straight edge and compass in finitely many steps. – TurlocTheRed Dec 23 '24 at 22:18
  • @TurlocTheRed Inefficient is an understatement! As mentioned, any rational approximation is theoretically achievable, but the condition is that it must be practical to draw. I'm not providing a precise threshold for the moment (I might think about it in some future), just common sense. – lesath82 Dec 24 '24 at 12:22

1 Answers1

7

In his 2022 Parabola article "Squaring the Circle like a Medieval Master Mason," Frédéric Beatrix introduced a geometrographic construction that is claimed to offer an improved approximation over previous methods.

Beatrix holds that his construction not only refines Ramanujan's approximation, but also improves on H.V. Chu's, presented in Chu's 2019 paper "Square the Circle in One Minute." He says (in the cited articl):

The accuracy of this approximation is 0.0007% - that is 7mm over one kilometre. The level of accuracy is the same as the approximation in Figure 4 by Hung Viet Chu. However, our construction requires only 13 steps and produces a very neat and elegant figure. For hand-drawn figures, this is the best solution for approximately squaring the circle to date.

The diagram below illustrates Beatrix's main idea:

Beatrix construction from Wikipedia

Tankut Beygu
  • 4,412
  • Thank you, I'm already upvoting your answer which is anyway useful. I'll read your reference in detail, but I get that they consider their idea as an improvement if one takes into account the amount of required steps, which introduce error when actually performed (using Lemoine's metrics). This is indeed an interesting topic (I already tried to deepen it, even here on MSE). But now my first requirement is to improve the absolute precision of the construction. – lesath82 Dec 23 '24 at 14:25
  • Lemoine's metrics for me have some important weaknesses. One (and not the only one) is that sometimes a few more steps can actually result in increased precision. Anyway they deserve credit for trying to supply some objective measure of the simplicity/exactness of a construction when actually hand-drawn. Within this framework, Beatrix's might be the best squaring you can actually draw: an absolutely legit and interesting quest, just a slightly different challenge than the one I'm focusing on. – lesath82 Dec 23 '24 at 14:34
  • I think you can directly converse with Dr Hamkins. He's been actively contributing to MathOverflow. I also follow him onTwitter (@JDHamkins). – Tankut Beygu Dec 23 '24 at 14:39
  • 1
    Thanks for the suggestion. I haven't subscribed to MathOverflow yet. I shall, of course, but I think I won't be allowed to reach out to a user directly, will I? Not having Twitter either (facepalm)... I'll wait for some reasonable time before cross-posting my question on MO, unless you can poke him on my behalf. – lesath82 Dec 23 '24 at 15:10
  • 1
    I gave a look at Chu's paper as well... there is, of course, the construction improved by Beatrix, but thereafter he proposes another one that shares my same goal! But I cannot agree when he says "our construction is at the same level of complexity of Ramanujan's" (and, in fact, he traces only partial portions of the procedure, describing then what the continuation should be). I'm updating my question with this new information, thank you! – lesath82 Dec 24 '24 at 14:22
  • I'm glad to be of help. – Tankut Beygu Dec 24 '24 at 15:30
  • The approximation $\pi\approx 6\phi^2/5$ is given by Ramanujan as $\pi\approx\frac{9}{5}+\sqrt{\frac{9}{5}}$. I wonder why he didn't give any construction based on it. – Paramanand Singh Dec 27 '24 at 08:49
  • @ParamanandSingh Maybe he was, as I am :-), fascinated by the pursuit of the maximum possible precision. I guess it had to be attainable —quoting Wikipedia— with a "particularly simple" construction (let me say, "elegant"), but he didn't care about relating it to some quantitative metric of the complexity. If this was the task, $\pi \approx \frac{9}{5} + \sqrt{\frac{9}{5}}$ is just much less precise even than $355/113$ (for which he gave a construction alternative to de Gelder's). As mentioned in a comment above, there is much taste involved in this topic. – lesath82 Dec 29 '24 at 21:40
  • @TankutBeygu Ramanujan had a version of this approximation to pi using the golden ratio. Kindly see this new post. – Tito Piezas III Feb 26 '25 at 11:26
  • 1
    @TitoPiezasIII thank you for letting me know. – Tankut Beygu Feb 26 '25 at 13:54