8

I was trying to assess the impact of non-idealities on the outcome of a classical geometric construction, performed on paper with actual compass and straightedge.

I was thinking of possible approaches, but at the same time I didn't want to start from scratch, expecting that someone must have investigated this topic before me.

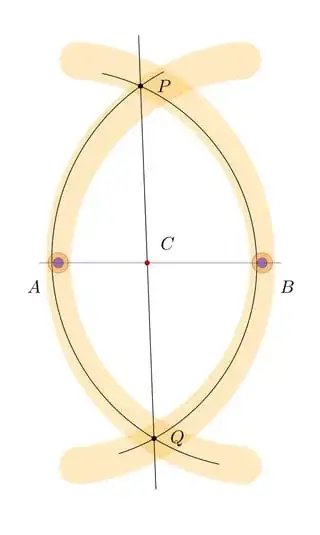
In fact I found this article. I seem to find only this article. The author hits the core, he perfectly delineates the matter, and in particular he includes images that are pretty self-explanatory:

enter image description here

Unluckily he develops the discussion in qualitative terms and does not offer a useful framework. Near the ends he writes "The goal might be to mount a precise analysis of all the standard constructions and compare competing constructions for accuracy. There is a literature of papers doing precisely this, and I will try to post some references later", but apparently he could not recall what such references were.

Can anybody help me on this subject, suggesting methods or texts? Thank you!

lesath82
  • 2,605
  • A fun question - I've been amazed at how badly some of my constructions come out, even simple ones! If you're interested in the kinds and range of non-idealities, there are studies in teachers, even when they're using software, e.g. https://files.eric.ed.gov/fulltext/EJ1169844.pdf. If you're interested in the propagation through steps, you might consider the literature on errors in machining parts, for which positioning lead on paper would be a restricted case. – RobinSparrow Mar 07 '24 at 20:24

1 Answers1

2

You will find some discussion of these issues in

J. Wallner, R. Krasauskas, H. Pottmann, "Error propagation in geometric constructions", Computer-Aided Design Volume 32, Issue 11 (2000), pp. 631-641.

Moishe Kohan
  • 111,854
  • Thanks! This paper starts describing EXACTLY the kind of problem I hoped to tackle, but then proceeds towards methods and entities that I wouldn't be able to use for my purpose. I mean, I was hoping to be able to assess how imprecise it might get, say, a regular pentagon when drawn with compass and straightedge. I fear that this sentence from the paper's conclusion implies that I was too optimistic: "The aim of the paper [...] to demonstrate how much more difficult error propagation problems become if one uses a richer geometry such as the Euclidean one compared to planar affine geometry." – lesath82 Mar 08 '24 at 00:20