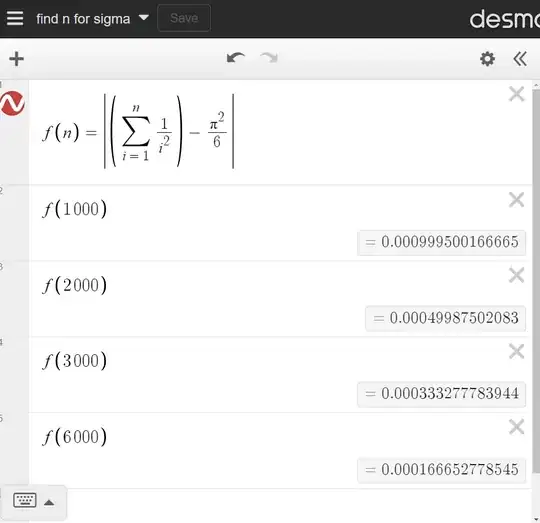
Could you help me, the task is to determine the number of terms needed to sum up to reach accuracy of 5 decimal places. The series is: $\sum_{n=1}^{\infty}{\frac{1}{n^2}}$
I have seen that $\sum_{n=1}^{\infty}{\frac{1}{n^2}}=\frac{\pi^2}{6}$, but this isn't excatly what I want but may be this will useful somehow, I don't have any good ideas how to start