Visual intuition for normal subgroups

Question

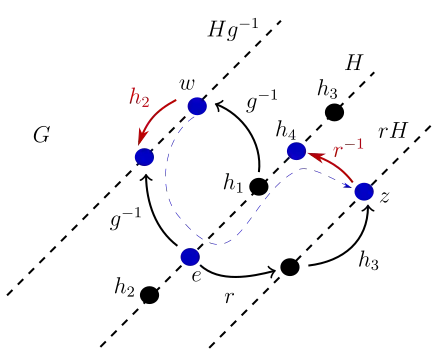
I've read this discussion on Intuition behind normal subgroups, but I'm still unable to create a mental picture of what is going on behind the scenes. I'm trying to build an alternative visualization. For a finite group $G$, a subgroup $H \subset G$ is said normal if satisfies: $$ gH = Hg, \forall g \in G \tag{1} $$ My goal with this question is to come up with a visual interpretation for (1). Let's consider two arbitrary cosets for $G$, $Hg^{-1}, rH$. The cosets are shown below, including their respective representatives $w$ and $z$.

I'm guessing that if we have (the red arrows in the figure): $$ \begin{align} w^{-1} g^{-1} \in H \\ z r^{-1} \in H \end{align} \tag{2} $$ Then, we can build the following path (shown in blue in the figure): $$ gH rH = w^{-1}z = h_{2} g h_{4}r \tag{3} $$ My intuition says that (2) and (3) should be enough to prove (1), but I'm stuck at this moment. This strategy makes any sense at all?

---

Edit

I ended up reading this beautiful post with some motivation behind normal subgroups. After reading it and with the comments of @JohnDouma, I came up with another view of the problem.

I understood the main idea as follows. Let $gH$ be an arbitrary coset whose representative is $[g]$. For the set of representatives form a group we need: $$ [g] \circ [g^{-1}] = [e] \tag{4} $$ Eq. (4) implies that for any two representatives in $\{ [g], [g^{-1}], [e]\}$ the third is determined.

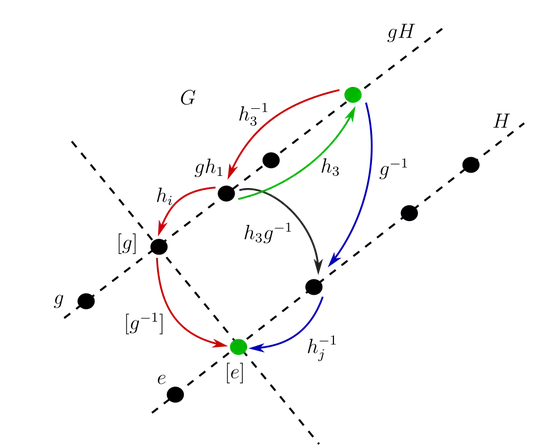
Note that given $gh_{1} \in gH$, and $h_{2} \in H$, even if $H$ is not normal, we have the following condition (illustrated on the left of the figure below): $$ gh_{1} \circ \underbrace{ (h_{1}^{-1} g^{-1} h _{2}) }_{ r } = h_{2} $$

Now, if $H$ is normal, Eq. (4) implies that for any representative in $[g]$ and $[e]$ we can still create another path which coincides with $r$, which is also shown on the left of the above figure.

In particular, we can think that the simplest description for $r$ will appear when the representative of $[g]$ is $gh_{1}$ and the representative of $[e]$ is $h_{2}$. This implies that $r \in [g^{-1}]$, say $r = h_{3}g^{-1}$, and: $$ \begin{align} g h_{1} \circ h_{3} g^{-1} = h_{2} \implies \\ g h_{4} = h_{2} g \end{align} \tag{5} $$ which implies (1).

To see more clearly why the elements of $g$ are said to commute with $H$, we can replace $r$ in the left figure by $h_{3}g^{-1}$. The new obtained figure is shown below:

Then, after a translation by $h_{3}$, we find that there are two paths that connect the green points: the red and blue, which implies:

$$ \begin{align} h_{3}^{-1} \circ h_{i} \circ (h_{k}g^{-1}) = g^{-1} \circ h_{j}^{-1} \implies h_{l} g^{-1} = g^{-1}h_{m} \end{align} \tag{6} $$

Answer 1

As someone who spent a few years trying to understand this part of algebra more visually I have two comments:

• Equation (1) tells you nothing about the internal structure of $H$ -- if you use the phrase "element of $H$" in setting up or describing your picture, you are not capturing the content of equation (1).

• Equation (1) does tell you about the partitioning of $G$ by cosets of $H$ -- so you should be thinking of $G$ partitioned into pieces congruent to $H$ in two different ways (as left cosets and as right cosets), with a miraculous two-part coincidence:

  • The two partitions are into the same subsets.
  • Each element of $g$ takes $H$ to the same left and right coset.

  That is, generically, the subsets of $G$ that are left cosets of $H$ need not be the same as the subsets of $G$ that are right cosets of $H$. That they are the same subsets is a coincidence of note. Also, we can label each left coset by the element of $G$ such that $gH$ is that coset. And we can label the right cosets the same way. With the coincidence of partitions of $G$, each subset is labelled with two collections of elements of $g$. The second coincidence is that the two collections are equal in every subset.

The picture I ended up with (to capture the factorization by normal subgroups) was to have $H$ be a vertical column in a 3-dimensional array (usually on the closest corner so it is easy to see), each other column is a coset of $H$ (and we don't have to specify whether the columns are left cosets or right cosets, because "yes"), and the slices perpendicular to $H$ are cosets of $G/H$. The slice containing $e$ is a set of representatives of $G/H$ in $G$. The other slices are cosets of $G/H$, but the second coincidence fails: which elements of $H$ take the $e$-slice to that slice on the left and on the right need not be the same. (If the cosets of $G/H$ do have the second coincidence, then $G$ is the direct product of $H$ and $G/H$. There are many examples of groups having normal subgroups for which this second coincidence does not occur.)

Here, the elements of $G$ in a coset of $H$ are the same color. This is a busy image, and I think a better artist could pick colors to help the eye more than I did. The $eH$ and $He$ coset are of course the elements of $H$. For any coset of $H$, say $g_1 H$, $g_1$ is in $g_1 H$ because $g_1 e = g_1$. Likewise, every element of that coset takes $H$ to that coset. One of the normalcy coincidences can be explained on this diagram: $g_1 H$ ca be as shown, but $H g_1$ can lie at a slope through $g_1$, say $(1,0,1)$; then $g_1 H \neq H g_1$ (and "projection along $H$" has a left version and a right version that produce different partitions of $G$, so $H$ isn't normal). Then the process of quotienting by $H$ crushes everything onto the $xy$-plane -- each coset of $H$ crushes to one element of $G/H$ -- we've picked a set of representatives, one from each coset, the ones that happen to be in the $e$-plane perpendicular to $H$. (Note that this choice is "generic": you can permute the elemets of $G$ in any coset of $H$ and still get the same picture, with the option to have a different representative of the coset.) Finally, if $H$ and/or $G$ are big, one should allow the diagram to continue off as much as needed in the $x$-, $y$-, and/or $z$-directions.

In reality, neither $H$ nor $G/H$ should really be considered one-dimensional or two-dimensional, since either could decompose into various kinds of products of their various normal subgroups. (See group extension, where a 2-dimensional version of the above diagram appears. Don't worry about the details of short exact sequences. That one says that $N$ is a subgroup of $G$ and $G/N$ is a group, so $N$ is a normal (otherwise the left and right cosets don't mesh to let $G/N$ as a set form a group) factor of $G$.)

Also, you will eventually want to understand "characteristic", a sort of "super-normal". You will get a lot farther with visual understanding if you re-write equation (1) as $$ gHg^{-1} = H \text{.} $$ capturing a different aspect of normalcy. The object on the left is the conjugate of $H$ by $g$. These provide a different partitioning of $G$ and both normalcy and charistic-ness are easier to compare and contrast in terms of this partitioning.