2

$$\tag{1}f(\theta,\phi) = \cos\theta e^{i\phi}$$

By observation of the complex exponential, we can immediately see that $m = 1$, and we know that $|l|\le m$.

When attempting to create a spherical harmonic expansion representation of the function $$f(\theta,\phi) = \sum_{l=0}^\infty\sum_{m=-l}^l f_l^m Y_l^m(\theta,\phi)$$ where we recognize that the spherical harmonics $Y_l^m(\theta,\phi)$ form a complete orthonormal set of functions which allows us to identify the coefficients as $$f_l^m = \int_0^{2\pi}\int_0^\pi f(\theta,\phi)Y_l^{m*} \sin\theta d\theta d\phi$$ we get (the associated form):

$$\tag{2}xe^{i\phi}= f_0^0Y_0^0 + f_1^{-1}Y_1^{-1} + f_1^0Y_1^0 + f_1^1Y_1^1 +...$$

recalling that $m = 1$ and recognizing that $l\ne0$ by observation, we eliminate coefficients in (2) to get:

$$\tag{3}xe^{i\phi} = f_1^0Y_1^0 + f_1^1 Y_1^1$$

Working through (3), I end up at:

$$xe^{i\phi} = f_1^0N_1^0 x - f_1^1N_1^1\sqrt{1-x^2}e^{i\phi} \\ x\Big(f_1^0N_1^0-e^{i\phi}\Big) = f_1^1N_1^1\sqrt{1-x^2}e^{i\phi}$$

And I'm not sure what to do from here or if there is anything I can do. I don't want $\phi$ or $\theta$ in the definitions of my constants, but I don't see how I would avoid that. Is there a way to evaluate these coefficients to satisfy the spherical harmonic expansion representation of this function?

J. W. Tanner
  • 63,683
  • 4
  • 43
  • 88
Researcher R
  • 807
  • 1
    Presumably you mean $\cos(\theta)e^{i\phi},$ not $\cos(\theta e^{i\phi})?$ Better to clarify. – Thomas Andrews Dec 03 '24 at 03:23
  • 1
    If the former, you can also clarify by writing $e^{i\phi}\cos\theta.$ – Thomas Andrews Dec 03 '24 at 03:26
  • I think you mean $|m|\le l$. And this question is closely related to: https://math.stackexchange.com/q/4997738/715329. While there’s no answer there, the comments essentially address the question. – Pranay Dec 03 '24 at 03:27

1 Answers1

4

Yes there is, with $Y_l^m(\theta,\phi)\propto e^{im\phi}P_l^m(\cos\theta)$, absorbing the normalisation constant into $a_n$:

\begin{align}e^{i\phi}\cos\theta &= \sum_{n=1}^\infty c_n Y_{2n}^1(\theta,\phi)\\&= \sum_{n=1}^\infty a_ne^{i\phi}P_{2n}^1(\cos\theta) \end{align}

with $l=2n$, noting that the coefficients are zero for odd $l$ [as $P_{2n+1}^1(x)$ is even]. As @Pranay said in a comment, $l\ge|m|$, not $l\le|m|$.

The coefficients $a_n$ are given by (more details at the end)

\begin{align} \frac{a_n}{-\pi} &=\frac{(4 n + 1)(2 n - 1)!}{-2\pi(2 n + 1)!}\int_0^\pi \sin\theta d\theta P_{2n}^1(\cos\theta)\cos\theta\\ &=\binom{-\tfrac12}{n}^2\frac{n+\frac14}{(n+1)(2n-1)}\\ &= \frac5{2^5}, \frac9{2^8}, \frac{65}{2^{12}}, \frac{595}{2^{16}},\frac{3087}{2^{19}},... \:n=1,2,3,4,5,... \end{align}

Here is a plot from the first 5 terms.

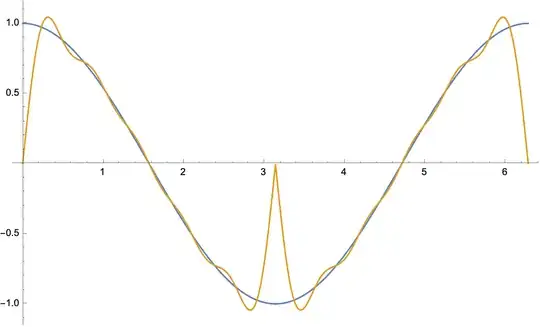
first 5

and for the first 50 terms, the Gibbs phenomenon is evident:

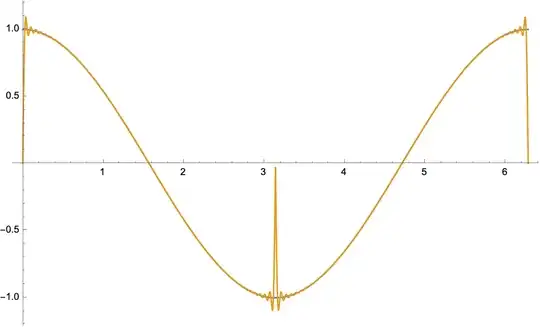
first 50

Edit: more details on $a_n$, with $x=\cos\theta$, also using https://en.wikipedia.org/wiki/Legendre_polynomials for the explicit form of $P_{2n}(x)$. \begin{align} J_n &= \int_0^\pi \sin\theta d\theta P_{2n}^1(\cos\theta)\cos\theta\\ &= \int_{-1}^1 dx P_{2n}^1(x)x\\ &= -\int_{-1}^1 dx \,x\sqrt{1-x^2}\frac{d}{dx}P_{2n}(x)\\ &= \int_{-1}^1 dx \,\frac{1-2x^2}{\sqrt{1-x^2}}P_{2n}(x)\\ &= \frac1{2^{2n}}\sum_{k=0}^n (-1)^k \binom{2n}{k} \binom{4n-2k}{2n}\int_{-1}^1 dx \,\frac{1-2x^2}{\sqrt{1-x^2}}x^{2(n-k)}\\ &= \frac1{2^{2n}}\sqrt\pi\sum_{k=0}^n (-1)^k \binom{2n}{k} \binom{4n-2k}{2n}(k-n)\frac{\Gamma(\frac12-k+n)}{\Gamma(2-k+n)}\\ &= -\frac{n}{2^{2n}}\sqrt\pi\binom{4n}{2n} \frac{\Gamma(\frac12+n)}{\Gamma(2+n)}S_n\\ S_n &= \sum_{k=0}^n b_k\\ b_0 &= 1\\ \frac{b_{k+1}}{b_k} &= -\frac{(n - 1 - k)(n + 1 - k)}{(2 n - \frac12 - k)(1 + k)}\\ b_k &= (-1)^k\frac{(n-1)_k(n+1)_k}{(2n-\frac12)_k k!}\\ &= \frac{(1-n)^{(k)}(-1-n)^{(k)}}{(\frac12-2n)^{(k)}k!}\\ S_n &= {}_2F_1(1-n,-1-n;\frac12-2n;1)\\ &= \frac{\sqrt\pi\Gamma(\frac12-2n)}{\Gamma(-\tfrac12-n)\Gamma(\frac32-n)}\\ J_n &= -\frac{n}{2^{2n}}\pi\binom{4n}{2n} \frac{\Gamma(\frac12+n)}{\Gamma(2+n)} \frac{\Gamma(\frac12-2n)}{\Gamma(-\frac12-n)\Gamma(\frac32-n)}\\ &= -\frac{\pi^2}{\Gamma(-\frac12-n)\Gamma(\frac32-n)\Gamma(n)\Gamma(n+2)}\\ \frac{a_n}{-\pi} &= \frac{n + \frac14}{n(2 n + 1)} \frac{\pi}{\Gamma(-\frac12-n)\Gamma(\frac32-n)\Gamma(n)\Gamma(n+2)}\\ &=\binom{-\tfrac12}{n}^2\frac{n+\frac14}{(n+1)(2n-1)} \end{align} using \begin{align} \frac{\pi}{\Gamma(-\frac12-n)\Gamma(\frac32-n)} &= \frac{2n+1}{2n-1}\frac{\pi}{\Gamma(\frac12-n)^2}\\ &= \frac{2n+1}{2n-1}\binom{-\frac12}{n}^2(n!)^2 \end{align}

Edit: Some more detail on the integral the OP queried. Might've been easier to not switch to $x=\cos\theta$ and back.

\begin{align} I_{2m} &= \int_{-1}^1 dx \,\frac{x^{2m}}{\sqrt{1-x^2}} &= \int_0^\pi d\theta \cos^{2m}\theta \end{align} which is easy using, $I_0=\pi$ and $I_{2m}=\frac{2m-1}{2m}\frac{2m-3}{2m-2}\ldots I_0 = \frac{\Gamma(m+\frac12)/\Gamma(\frac12)}{\Gamma(m+1)}\pi$ e.g. from Prove $\int\cos^n x \ dx = \frac{1}n \cos^{n-1}x \sin x + \frac{n-1}{n}\int\cos^{n-2} x \ dx$

So \begin{align} \int_{-1}^1 dx \,\frac{1-2x^2}{\sqrt{1-x^2}}x^{2(n-k)} &= \frac{n-k+1-2(n-k+\frac12)}{n-k+1}\frac{\Gamma(n-k+\frac12)}{\Gamma(n-k+1)}\sqrt\pi\\ &= (k-n)\frac{\Gamma(n-k+\frac12)}{\Gamma(n-k+2)}\sqrt\pi \end{align}

Ramashalanka
  • 1,113
  • If it isn't too much trouble, then yes I would like to some additional details to help break down your process. I think that would help me, and thank you! – Researcher R Dec 04 '24 at 23:42
  • Or at the very least, how you came to that form for the Legendre polynomial. I only just now found out about the closed form of the Legendre Polynomial today. It sounds like you have your own method for how you arrived to your own closed form. So you took the open term (given $l = 2n, m = 1$) $$\frac{d^{2n}}{dx^{2n}}(1-x^2)^{2n}$$ and turned it into some series (not sure which type of series from just looking at it) representation, I'm just not sure on the specifics. Would be interested to see how you did that too if it's not too much trouble. – Researcher R Dec 04 '24 at 23:56
  • Thank you! This helps a lot. The real challenge for me is going to be integrating an integral of the form $$\int_{x_0}^{x_1} \frac{(a-bx^2)}{\sqrt{a-cx^2}}x^{2d} dx$$ which appears in the 4th line of your workings. Looks fairly daunting. – Researcher R Dec 05 '24 at 02:34
  • Rewriting the binomial expansions as gamma functions gives me $$\sum_{k=0}^n (-1)^k (n-k) \frac{\Gamma(4n-2k+1)\Gamma(1/2-k+n)}{\Gamma(k+1)\Gamma(2n-k+1)\Gamma(2n-2k+1)}$$. I’ve noted from writing out 7 successive terms that $$\frac{(4n-2k)!}{(2n-k)!}$$ cancels out every other term and leaves a 2, and I’m guessing we’d have a double factorial left over. Beyond that, I am simply too outside of my depth to figure out what else could be done to reduce this further much less remove k. Could you provide some intermediary steps? – Researcher R Dec 08 '24 at 21:13
  • Everything works out, just took me a while to verify. I just have one last question and it's about the normalization constant multiplied by our integral. So for $l=2n,m=1$, using the spherical harmonic definition $Y_l^{m*}(\theta,\phi)=\sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^m e^{im\phi}$ I get, $$c_{n}^1 = N_{2n}^1\int_\Omega \cos\theta P_{2n}^{-1}(\cos\theta)d\Omega$$, and if $a_n = N_{2n}^1c_n$, then $$a_n = (N_{2n}^1)^2 \int...d\Omega$$ and therefore: $$\frac{a_n}{-\pi} = \frac{4n+1}{-4\pi^2}\frac{(2n-1)!}{(2n+1)!}\int...d\Omega$$. So, I'm missing a $2\pi$ multiplier somewhere. – Researcher R Dec 17 '24 at 03:37
  • 1
    My integral is just the $d\theta$ integral. $d\Omega$ also includes the $d\phi$ integral, i.e. $\int_0^{2\pi} e^{-i\phi}e^{i\phi}d\phi = 2\pi$. – Ramashalanka Dec 17 '24 at 04:27
  • 1
    Knew it was something simple I was overlooking. Everything works out just fine then. Thank you! – Researcher R Dec 17 '24 at 05:19
  • You're welcome. Are you happy with how to do $\sin\phi$ for https://math.stackexchange.com/questions/4997738/how-to-represent-cos-theta-sin-phi-as-a-linear-combination-or-expansion-of-s ? Care with the normalisation for $m<0$ is the only thing. – Ramashalanka Dec 17 '24 at 06:48
  • I took some time to figure out how to perform the spherical harmonic expansion of Green's function and performing the convolution to solve for Poisson's Equation, and I finally just got back to this. I tried to find the coefficients for the case $m<0$ and I keep getting a sign error. $$\cos e^{i\phi} = e^{i\phi}\sum\sum c_l^1 N_l^1 P_l^1 = e^{i\phi}\sum a_l^1 P_l^1$$ and $$\cos\theta e^{-i\phi} = e^{-i\phi}\sum c_l^{-1} N_l^{-1} P_l^{-1} = (-1)^1 e^{-i\phi}\sum c_l^{-1}N_l^1 P_l^1 = -e^{-i\phi}\sum a_l^{-1} P_l^1 $$ which gives $$\sum a_l^{-1}P_l^1=\sum a_l^1P_l^1$$ gives $a_l^{-1} = -a_l^1$ – Researcher R Jan 12 '25 at 01:31
  • nevermind, plugging this in we get $$-e^{-i\phi}\sum(-a_l^{1})P_l^1$$ so the negative signs cancel. So if I map this onto our exact problem $$\cos\theta e^{-i\phi} = e^{-i\phi}\sum \Bigg[-\pi\binom{-1/2}{n}^2\frac{n+\frac{1}{4}}{(n+1)(2n-1)}\Bigg]$$. Now the series converges to $\sin\theta e^{-i\phi}$. I find it odd that I end up with the exact same coefficients between $\cos\theta e^{i\phi}$ and $\cos\theta e^{-i\phi}$ – Researcher R Jan 12 '25 at 04:33