Deleting vertices of odd degree from a graph

Question

Let $H$ be a graph, all of whose vertices have even degree. We construct a new graph $H'$, isomorphic to the first one, with $V(H)=\{v_1,v_2,...,v_n\}$ and $V(H')=\{v_1',v_2',...v_n'\}$ disjoint. Next, we construct a graph $G_0$, such that $V(G_0)=V(H)\cup V(H')$ and $\{u,v\}\in E(G_0)$ if and only if:

• $\{u,v\}\in E(H),$
• $\{u,v\}\in E(H'),$ or
• $\{u,v\}=\{v_i,v_i'\}$ for some $i$.

This $G_0$ is our initial graph. In a single operation, we take a vertex of $G_j$ with odd degree and delete it, together with all of its edges, to form a new graph $G_{j+1}$.

For each initial graph, is it possible to find a sequence of moves such that $G_j$ has no edges?

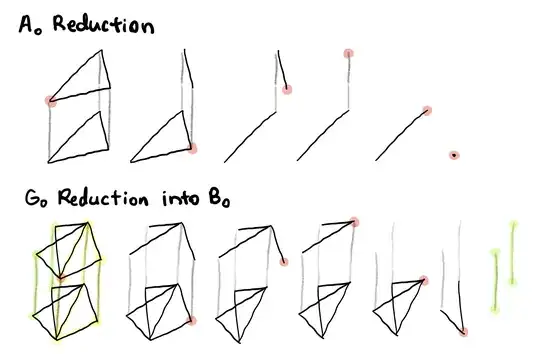
For example, observe the following graph $G_0$, generated by a triangle graph $H$ with $V(H)=\{1, 2, 3\}$:

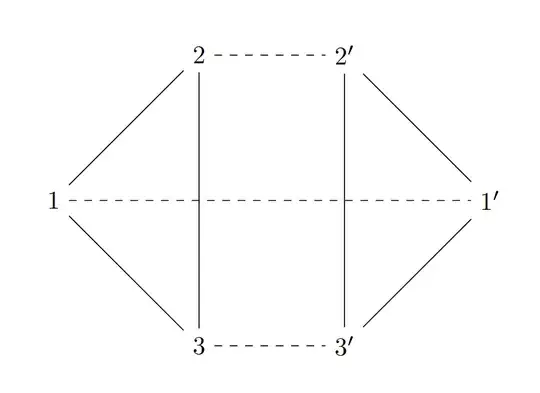
Say we delete vertex $1$, which is allowed as $\deg (1)=3$ is odd. We get graph $G_1$:

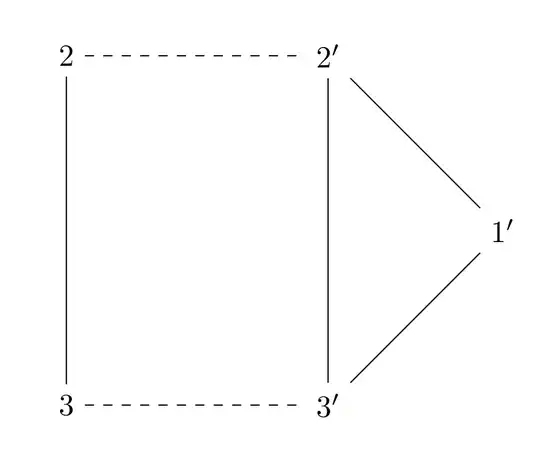
Now we delete $2'$ to get the graph $G_2$: $2-3-3'-1'$. We delete $2, 3, 3'$ to get the graphs $G_3, G_4, G_5$ respectively. We are left with $G_5$, which consists only of $1'$.

This problem is a stronger form of IMO Shortlist 2013 C3., where only one application of $(ii)$ is allowed (and this is how I came across this problem).

I tried using induction to prove we can always reduce a graph to one with a lesser chromatic number, but this approach breaks down if one accidentaly deletes a vertex which results in the subsequent graph having all degrees even (for example, a complete graph with $5$ vertices.)

Intuition tells me that this result should hold, as for small graphs $H$, it works for all of them, and for bigger and bigger graphs, we always have a large supply of vertices with an odd degree.

The problem seems much harder that the original problem from the shortlist, so I'm excited to see your observations and insights. Maybe someone finds a counterexample!

---

Update: An idea that comes to mind is to find a characterization of a reducible graph, that is, a graph (which need not be connected) for which there exists a finite sequence of operations which reduces it to a graph without edges. After we find a characterization, we may inductively assume that a graph with $n-1$ vertices with that characterization is reducible. Then we observe an arbitrary graph with $n$ vertices and try to find a vertex, which after being removed results in a graph which once again satisfies the characterization. The problem arises when we try to explicitly find a characterization (i.e., a condition equivalent to being reducible).

Naively, I came up with the following characterization for irreducible graphs:

A graph is irreducible if and only if when partitioned into connected components $G_1, G_2, ..., G_k$, some subgraph $G_i$ contains at least one edge, and either:

1. $G_i$ has only vertices of even degree, or
2. $G_i$ is a complete graph with an even number of vertices.

Upon further investigation, this characterization is flawed. For example, if we take two triangles and connect them by an edge, that graph is also irreducible. Really, we can make chains of any length with these triangles. Notice that we can do the same thing with any graph with all degrees even, not just with triangles!

If we replace condition $1$ with "$G_i$ is a chain of graphs with vertices of even degree", this characterization is still flawed, as there are irreducible graphs which don't satisfy it.

Maybe this is a dead end. Maybe not?

Answer 1

For a graph $G$, define $f(G)=G\times K_2$ (i.e. your "doubling" process). Note that $f(H)=G_0$. We call a graph even if all vertices have even degree, and say a graph $G$ can be partitioned into $G_1$ and $G_2$ if $G_1$ and $G_2$ are the induced subgraphs on two disjoint vertex sets whose union is the vertex set of $G$.

Our proof will use strong induction on the number of vertices of $H$. The base case of one vertex is trivial. We now assume all even graphs with order $<|H|$ are reducible, and note that we only need to focus on connected graphs since we can automatically split up disconnected graphs into smaller components. We'll start with a couple lemmas:

---

Lemma 1: Any graph $H$ can be partitioned into even subgraphs $H_1$ and $H_2$. If $H$ is not even, then both $H_1$ and $H_2$ are not zero-order.

Proof: The first part follows from here. For the second part, if $H$ is not even, then one of $H_1$ or $H_2$ being zero-order implies the other is $H$ (which is not even), a contradiction.

---

Lemma 2: If a connected even graph $H$ can be partitioned into nonzero-order $H_1$ and $H_2$, where $H_1$ is even, then we can perform a sequence of moves that reduces $G_0=f(H)$ into $f(H_2)$.

Proof: Define $A_0=f(H_1)$ and $B_0=f(H_2)$. From our inductive hypothesis, $A_0$ is reducible, and say this is possible by deleting the vertices of $A_0$ in some order $v_1,v_2,\dots, v_n$. Letting $A_i$ denote $A_0$ after $i$ deletion steps, the problem constraint guarantees that $\deg_{A_{i-1}}(v_i)$ is odd.

We aim to show that we can delete $v_1,v_2,\dots, v_n$ in that order from $G_0$ as well, or equivalently that $\deg_{G_{i-1}}(v_i)$ is odd. Note that $\deg_{G_0}(v_i)-\deg_{A_0}(v_i)$ is even since $H$ and $H_1$ are even. Now, consider the edges in $G_0$ but not in $A_0$ that have a vertex at $v_i$ (i.e. the edges that contribute to the degree difference). These edges must have their other vertex in $B_0$, so during the deletion process they cannot be deleted before $v_i$ is deleted. Hence, the degree difference is preserved, meaning $\deg_{G_{i-1}}(v_i)-\deg_{A_{i-1}}(v_i)$ is even. But since $\deg_{A_{i-1}}(v_i)$ is odd, $\deg_{G_{i-1}}(v_i)$ is odd too.

Hence, we delete $v_1,v_2,\dots, v_n$ from $G_0$ to reduce it to $B_0$, as desired. An example is shown below, with $A_0$ in yellow and $B_0$ in green. Indeed, the reduction process of $A_0$ confers to that of $G_0$.

---

Now for our inductive step. We consider two cases:

Case 1: $H$ is a cograph.

If $H$ is a cograph, then there exists two vertices $u$ and $v$ that have the same (closed or open) neighbor set. We partition $H$ into $\{u,v\}$ and $H'=H\setminus\{u,v\}$ (the case of $H'$ being zero-order is trivially resolved). If there is no edge between $u$ and $v$, Lemma 2 says that we can reduce $G_0$ into $f(H')$. If there is an edge between $u$ and $v$, then we can delete $u, v’, v, u’$ in that order from $G_0$ to reduce it to $f(H')$, where $u’$ and $v’$ are the respective corresponding vertices of $u$ and $v$ in the doubled graph. But note that if a vertex's degree is impacted by deleting $\{u,v\}$ from $H$, the degree must decrease by $2$ since being connected to one of $\{u,v\}$ means being connected to the other. Hence, $H'$ is even, so $f(H')$ can be reduced as per our induction hypothesis. It follows that $G_0$ is reducible.

Case 2: $H$ is not a cograph.

This condition implies that there exists some set of $4$ vertices in $H$ that induces a $P_4$ path graph. Let $Q=H\setminus P_4$, which is not zero-order. If $Q$ is even, we finish by using Lemma 2 to reduce $G_0$ to $f(P_4)$, which can be easily checked to be reducible.

If $Q$ is odd, we use Lemma 1 to partition it into $2$ nonzero-order even subgraphs $Q_1$ and $Q_2$. Lemma 2 tells us that we can reduce $G_0$ into $f(H\setminus Q_1)$. Now, $H\setminus Q_1$ consists of $P_4$ with some number of connections to $Q_2$. Each vertex of $P_4$ has either an even (E) or odd (O) number of these connections. We check the following distributions of connections: EEEE, EEEO, EEOE, EEOO, EOOE, EOOO.

Any distribution symmetrical to one of these is automatically covered, and other distributions can be "swapped" into one of these. That is, since $Q_2$ is also even, we can look at the reduction of $G_0$ into $f(H\setminus Q_2)$ instead of $f(H\setminus Q_1)$ initially. Since the vertices of $P_4$ must have even degree in $H$, the connection parity for the starting and ending vertices of $P_4$ will swap, while the middle vertices' will be preserved (e.g. OEOE gets swapped to EEOO). An example is shown below: We now show that $f(H\setminus Q_1)$ (or $f(H\setminus Q_2)$ if we did a swapping) can be reduced into $f(Q_2)$ (resp. $f(Q_1)$). This occurs from deleting the vertices of $f(P_4)$ in some valid order. The ordering for each of our $6$ cases is shown below (first delete the vertex labled $1$, then $2$, etc.), with green corresponding to an even-connection vertex and orange corresponding to an odd-connection one:

All our reductions put together have now reduced $G_0$ into either $f(Q_2)$ or $f(Q_1)$, which are both reducible by our induction hypothesis. Hence, $G_0$ is reducible, and we are done.