This post gave a simple method to construct a parabola tangent to four given lines.
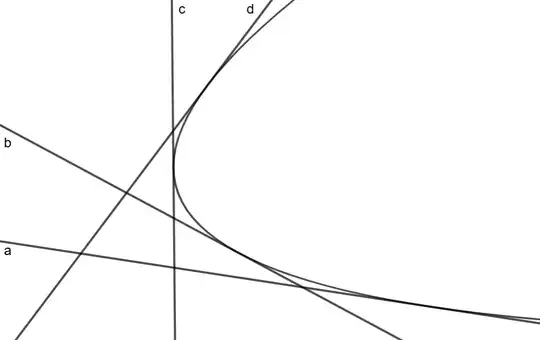
For four lines on the plane with distinct slopes, there is a unique parabola tangent to them. The parabola will be tangent to these lines at four points, which give the four lines an "order". For example, in the following figure, the four lines are tangent to a parabola in the order of $a,b,c,d$.
Let's write $\overline{a,b,c,d}$ if the four lines are tangent to a parabola in the order of $a,b,c,d$.
So any four lines with distinct slopes can be ordered in only two ways, $\overline{a,b,c,d}$ or $\overline{d,c,b,a}$.
My question is: For any five lines $a,b,c,d,e$ on the plane with distinct slopes,
If $\overline{a,b,c,e}$ and $\overline{a,c,d,e}$, does it imply that $\overline{a,b,d,e}$?
I tried to get a counterexample by drawing figures, but I didn't find one.
I guess the following is true:
$a,b,c,d$ form a concave quadrilateral in that order, is equivalent to $\overline{a,b,c,d}\vee\overline{b,c,d,a}\vee\overline{c,d,a,b}\vee\overline{d,a,b,c}$.
To check whether four lines form a concave quadrilateral, it is enough to check their slopes satisfy the inequality in The concave quadrilateral and the slopes of its sides , using this I proved a similar fact.
But an inequality in their slopes cannot distinguish $\overline{a,b,c,d}$ with $\overline{b,c,d,a}$, because when the lines are translated, their "order" changes cyclicly. For example, in the above figure, when $a$ is translated upward to the top, then the "order" becomes $\overline{b,c,d,a}$.