6

Draw $n$ random chords in a circle. Each chord connects two independent uniformly random points on the circle.

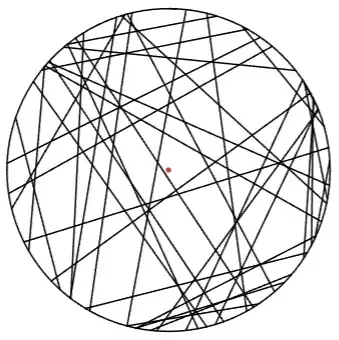
Here is an example with $n=40$.

enter image description here

In this example, the centre of the circle (shown in red) is contained by a pentagon.

Let $f(n)=$ expected number of sides of the polygon that contains the centre of the circle.

What is $\lim\limits_{n\to\infty}f(n)$?

(Ignore cases in which the centre of the circle is not contained by a polygon, i.e. is contained by a region with a curved edge.)

I tried, without success, to find the probability $P(n)$ that a random chord is collinear with a side of the centre-enclosing-polygon. Then the answer to the question would be $\lim\limits_{n\to\infty}nP(n)$.

Simulations

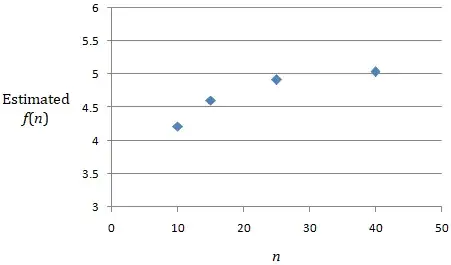
I used a random chord generator to run $50$ trials each with $n=10,15,25,40$, and made a graph.

enter image description here

EDIT: In the comments, @ArthurQueiroz provided data from $10^6$ trials up to $n=50$, yielding the following graph.

enter image description here

This is puzzling. Why would $f(n)$ go up, then down? Is there some issue with the simulation?

This is a follow-up question to the question "Draw $n$ random chords in a circle. What is the distribution of the kinds of polygons, as $n\to\infty$?"

Dan
  • 35,053
  • This is not defined, since the center may not be in a polygon – caduk Oct 20 '24 at 15:31
  • 2
    Results of my simulations + code: https://pastebin.com/raw/W4HVZZUG It also seems to me that f(n) approaches 5 as n goes to infinity

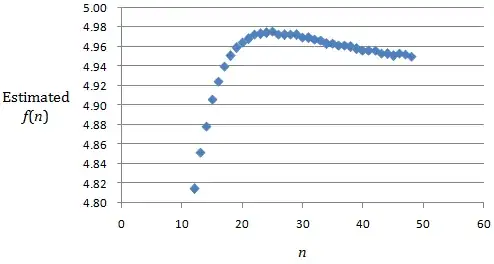
    .Although the results suggest that f(n) appears non-monotonic beyond a certain point, I believe that f(n) is actually monotonic. The issue likely stems from $10^6$ simulations being insufficient once n surpasses a certain threshold.

     – Arthur Queiroz Oct 21 '24 at 00:40
  • @ArthurQueiroz Thanks for the data. If $f(n)$ approaches exactly $5$, then the probability that a random chord is collinear with a side of the centre-enclosing-polygon, should approach $\frac5n$, which would be an elegant fact, maybe with an intuitive explanation. However, the data show a maximum around $n=27$ and then a fairly strong downward trend for $n>27$; and $10^6$ trials seems sufficient to show the true trend. I'm not convinced yet that $f(n)$ approaches $5$. – Dan Oct 21 '24 at 08:54
  • 2
    Your "random chord generator" may seem random, but it is not - at least not in the sense you define in the problem. Of course, neither is Arthur Queiroz's, but at least I know that the C psuedo-random number generator has been thoroughly tested and gives a reasonably good distribution. Added to the much larger sample size, his results have to be given preference over yours. One possible explanation for the decreasing $f(n)$ is that the chance for very short sides of the polygon increase with $n$, which then increases the chance that a new side may cut off 2 or more previous sides. – Paul Sinclair Oct 21 '24 at 22:09
  • @PaulSinclair Yes, Arthur's results are much more useful than mine. Good point about the increasing chance of very short sides. – Dan Oct 21 '24 at 22:16
  • Follow-up question: "The 'stained glass window problem': Draw many random chords in a circle; which kind of polygon ($3$-gon, $4$-gon, etc.) occupies the most total area?" – Dan Oct 22 '24 at 09:45

3 Answers3

4

(Self-answering)

The answer is $\dfrac{\pi^2}{2}=4.9348...$, according to this paper by Hilhorst and Calka. In section 1.2, there is a reference to a result by Matheron that the Crofton cell of a Poisson line process has average sidedness $\frac{\pi^2}{2}$.

I do not have access to Matheron's proof. Answers that include Matheron's proof, or any proof, would be welcome.

Dan
  • 35,053
0

Here is something. Not an answer, but too long for a comment.

Observation. As $n$ increases, most of the chords stop intersecting the central polygon. These chords don't matter for the asymptotic behavior of $f(n)$. If we, in each step, instead of choosing a random chord, chose a random chord that intersects the central polygon, we should get the same limit at the end.

Conjecture. If we reduce the circle's radius after each chosen chord so that it still contains the central polygon, the limit of the expected number of sides of the central polygon doesn't change.

This conjecture might not help with solving the problem analytically, but, if true, it surely helps with simulations, as we are now ignoring irrelevant chord choices.

Alma Arjuna
  • 6,521
  • We can show that the distributions of chords in the big and small circles are different. Assume the big circle has radius $R$, so the median length of its chords is $\color{red}{\sqrt2}R$. Now draw a very small circle of radius $r$ concentric with the big circle. Consider all the chords of the big circle that emanate from a fixed point on the big circle, and intersect the small circle. Within the small circle, these lines are almost parallel to each other and uniformly spaced. So the median length of the chords within the small circle is approximately $\color{red}{\sqrt3}r$. – Dan Oct 26 '24 at 01:59
0

This article considers the "the probability for the zero-cell to have n sides" for different random line arrangements in the plane: https://arxiv.org/pdf/0802.1869.
You might want to have a look, even though it does not exactly deal with the probability measure of random line arrangements you're interested in.

Andreas Rüdinger
  • 318