16

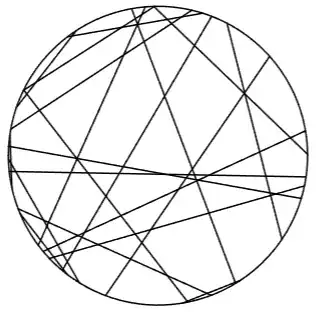
Draw $n$ random chords in a circle, where each chord connects two independent uniformly random points on the circle.

Here is an example with $n=20$:

enter image description here

In this example, there are $49$ polygons (I only consider the polygons with no chords going through them): $24$ triangles, $14$ quadrilaterals, $7$ pentagons, $4$ hexagons.

What is the limiting distribution of the kinds of polygons, as $n\to\infty$?

I made a random chord generator.

The average number of sides is $4$.

We can show that the average number of sides of the polygons is $4$, by the following argument.

Let $I=$ number of intersections, $G=$ number of polygons.

  • $\mathbb{E}(I)$ is the number of pairs of chords times the probability that two chords intersect, so $\mathbb{E}(I)=\frac16n(n-1)$.
  • This answer shows that the number of regions (including regions with curved edge) is $1+I+n$. Now $G$ dominates the number of regions with curved edge, so we can ignore the regions with curved edge. So $\frac{I}{G}\to 1$ as $n\to\infty$.
  • Each intersection is a shared vertex of $4$ polygons, so each one of those polygons "gets" $\frac14$ of that intersection. So each polygon should have on average $4$ vertices.

One elegant distribution that gives an average of $4$ would be: $\frac12$ triangles, $\frac14$ quadrilaterals, $\frac18$ pentagons, $\frac{1}{16}$ hexagons, etc. because $\sum\limits_{n=3}^\infty \frac{n}{2^{n-2}}=4$. I wonder if that distribution is the answer.

This question was inspired by the question, "On average, how many times must a circular pizza be randomly cut, to get a piece with no curved edge?"

Dan
  • 35,053
  • 1
    Follow-up question: "Draw $n$ random chords in a circle. What is the expected number of sides of the polygon that contains the center, as $n\to\infty$?" – Dan Oct 20 '24 at 22:27
  • Another follow-up question: "The 'stained glass window problem': Draw many random chords in a circle; which kind of polygon ($3$-gon, $4$-gon, etc.) occupies the most total area?" – Dan Oct 22 '24 at 09:45
  • 2
    just a small comment: Desmos has lists. You don't need to repeat the same function 40 times to draw 40 chords. Here's a version where you can move the number of chords up and down: https://www.desmos.com/calculator/nj28la7z59 – Alon Amit Oct 22 '24 at 23:58
  • @AlonAmit Thanks for the tip. It seems that the Desmos graph in your comment can only generate one set of random chords for each value of $n$. Is there a way to generate more sets of random chords for each value of $n$? – Dan Oct 23 '24 at 11:42
  • 1
    Another awesome question, @Dan ! Two (not very complete) thoughts: 1) clearly a useful thing here would be an algorithm to count the polygons for a given set of chords. Does anyone have any ideas for one? 2) Induction may help with both an analytical solution and such an algorithm. If a list of all polygons and their edges is known for $n$ lines, then it would be possible to calculate the intersections of these edges with the $n+1^\text{th}$ line and modify the polygon list accordingly. This is a bit beyond my coding skills but might be workable. – Chris Lewis Oct 23 '24 at 12:30
  • 3
    A thought: How does the problem behave when dilating and restricting the circle? E.g. if I take N chords in the circle of radius 2 and restrict to the circle of radius 1, is the resulting configuration of chords equivalent to one with uniformly random endpoints?

    I suspect that this doesn't work; however, if it does, then instead of chopping up the circle into finer and finer pieces, you can take larger and larger circles. In the limit, you should end up with a distribution of lines in the plane, which will likely have more useful symmetries than the original circle problem.

     – Greg Muller Oct 23 '24 at 13:36
  • 1
    @GregMuller I wonder if this might run into issues with the way the chords are chosen "at random" (as in the Bertrand Paradox. The random choice of lines in the plane may not be the natural one - although it might be interesting to think about transforming the circle into a "nicer" shape in such a way as to preserve the types of polygons formed. – Chris Lewis Oct 23 '24 at 15:19
  • 1
    @Dan in Desmos, at the top left, next to the + icon you use to add an expression, there's an icon with crossed arrows which refreshes the computation. Every time you click it you'll get a new set of chords. – Alon Amit Oct 23 '24 at 15:55
  • 2
    This indeed isn't invariant under dilation and restriction. However, in the limit as you consider a very small region of the circle it will be, though it won't be invariant to rotation. The limit in the centre will be invariant under rotation, however. And getting that distribution would be a major step towards Dan's follow up question about the distribution of the polygon containing the centre point, so the follow up question might be easier. – Zoe Allen Oct 23 '24 at 21:44
  • @GregMuller We can show that the distributions of chords in the big and small circles are different. Assume the big circle has radius $R$, so the median length of its chords is $\color{red}{\sqrt2}R$. Now draw a very small circle of radius $r$ concentric with the big circle. Consider all the chords of the big circle that emanate from a fixed point on the big circle, and intersect the small circle. Within the small circle, these lines are almost parallel to each other and uniformly spaced. So the median length of the chords within the small circle is approximately $\color{red}{\sqrt3}r$. – Dan Oct 26 '24 at 01:54
  • This paper has some results for a Poisson line process (which is different from the chords in this question). – Dan Oct 27 '24 at 14:03

2 Answers2

5

Best I have so far: At most $\frac{2}{3}$ of the polygons will be triangles.

Observation: In a generic arrangement of chords (no three chords pass through the same point), two triangles cannot be adjacent.

Why: If there were adjacent triangles, the opposite vertices in each triangle would both be intersection points between the same two lines. The parallel postulate disagrees.

In the large N limit, we can ignore the boundary regions. So, every edge of a triangle has a non-triangle on the other side, and therefore the total number of sides of triangles is at most the total number of sides of non-triangles. Letting $n_i$ denote the number of $i$-gons, $$3n_3 \leq 4 n_4 + 5 n_5 + 6n_6 + ...$$ As mentioned in the problem statement, the average number of sides is 4, so $$ \frac{3n_3 + 4n_4 + \cdots}{n_3+n_4+\cdots} = 4 $$ Combining the two gives $$ \frac{6n_3}{n_3+n_4+\cdots} \leq 4 \Rightarrow \frac{n_3}{n_3+n_4+\cdots} \leq \frac{2}{3} $$ It's worth noting that this argument is mostly combinatorial (rather than probabilistic), and it will remain valid for any configuration of chords in which $1/3$ of the pairs intersect and the number of boundary regions is negligible.

Greg Muller
  • 5,486
1

This article answers the question for a random line arrangement in the plane. The probability measure is a bit different from the one you consider but it might nevertheless be interesting for you: "Tanner, The Proportion of Quadrilaterals Formed by Random Lines in a Plane": https://www.jstor.org/stable/3213813.

Andreas Rüdinger
  • 318