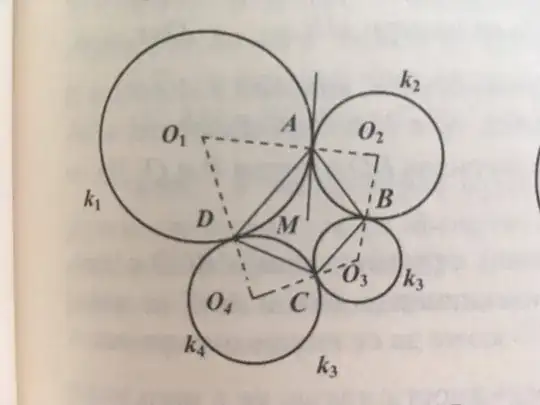
We consider following constellation of four circles tangent to each other:
Question: Are there some interesting relations between angles and ratios of inscribed quadrilaterals? Do they have specific "features"?
Two things are immediate: $\angle BAD = \dfrac{1}{2}(\angle DO_1A + \angle AO_2B)$ and analogously for others.
As consequence, the quadrilateral $ABCD$ has the feature to be a cyclic one, ie. its vertices lie on a circle.
But are there more interesting features of such constellation? Eg, what we know about structure quadrilateral $O_1O_2O_3O_4$? Is it a tangential quadrilateral? How to derive it from that $ABCD$ is cyclic?
Nitpick: If we specialize to constellation where additionally circle $k_1$ tangents circle $k_3$, can we then say something more?
(The "nitpick part" is a bit motivated by this question: The answer to problem adressed there is given analytically by finding intersection point of two hyperbola, but I wondering if one can argue directly analyzing angle relations of inscribed quadrilaterals.