Four Circles radii

Question

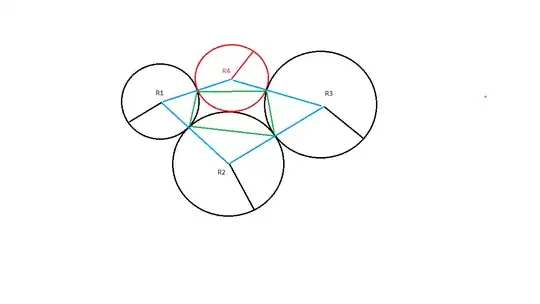
Consider following constellation of four adjacent circles.

Question:(Initial question doesn't give an unique solution; see edit) Assume we know the radii $R_1,R_2,R_3$. Is there a geometric/synthetic way to determine the radius $R_4$ of the red circle.

Ideas: I tried to draw auxilary lines and embedded the green and blue quadrilaterals. Using that each triangle inside each circle bounded by two blue and one green lines is an isosceles triangle, and from this it's easy to deduce that the opposite angles of the green quadrilateral add up to 180 deg. Note sure if that helps.

#EDIT: As Ethan Bolker & Lieven correctly observed, the radii of the three black circles not alone determine the red circle (neither its radius, not its position). Argument: There is "rolling degree" of freedom for left or right circles.

What, if we impose additional assumption by fixing a concrete angle of blue quadrilateral at at center of $R_2$. Can we then determine $R_4$ and the angles of blue quadrilateral at center of $R_4$?

Answer 1

No, in fact you can construct such a diagram for any four given positive lengths $R_1,$ $R_2,$ $R_3$ and $R_4.$ First draw $C_1$ with radius $R_1.$ Choose the centre of $C_2$ anywhere on the circle with the same centre as $C_1$ and radius $R_1+R_2.$ Then around those two centres draw circles with radii $R_1+R_4$ resp. $R_2+R_4,$ which must necessarily intersect in two points. Make one of those points the centre of $C_4.$ Finally draw circles around the centres of $C_2$ and $C_4$ with radii $R_2+R_3$ resp. $R_4+R_3.$ Those circles intersect in 2 points on either side of the line connecting their centres: choose the one on the opposite side from the centre of $C_1$ as the centre of $C_3.$

If in addition the angle at $P_2,$ the centre of $C_2$ is given, then $P_4$ and $R_4$ are uniquely determined by the conditions that:

$$d(P_2,P_4)-d(P_1,P_4)=R_2-R_1$$ $$d(P_3,P_4)-d(P_2,P_4)=R_3-R_2$$ $$d(P_3,P_4)-d(P_1,P_4)=R_3-R_1$$

Each of these conditions separately puts $P_4$ on a hyperbola: the locus of points with a given difference in distance to two fixed points. Only 2 out of the 3 conditions are independent, as the third is actually the sum of the first 2. The intersection of these hyperbolae determines $P_4$ and then $R_4$ is the distance from $P_4$ to any of the 3 other circles.

For an actual construction with ruler and compass, have a look at this question and answer.

Answer 2

Here is an "algebraic understanding" of the issue.

It uses the Cayley-Menger determinant which, equalized to $0$, gives a relationship between the mutual distances $d_{ij}$ of four points in the plane :

$$\det\pmatrix{ 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & d_{12}^2 & d_{13}^2 & d_{14}^2\\ 1 & d_{12}^2 & 0 & d_{23}^2 & d_{24}^2\\ 1 & d_{13}^2 & d_{23}^2 & 0 & d_{34}^2\\ 1 & d_{14}^2 & d_{24}^2 & d_{34}^2 & 0 } = 0\tag{1}$$

Here, contact conditions yield $d_{ij}=r_i+r_j$ but for $d_{13}$ that we name $d$, Let us plug these relationships into (1) and take for example $r_1=r_2=r_3=1$. The expansion of the determinant gives :

$$-2d^2(d^2r_4^2 +2d^2r_4 +d^2 -16 r_4^2 -32 r_4)=0$$

from which the following expression can be deduced :

$$d = 4 \frac{\sqrt{r_4^2 + 2r_4}}{r_4 + 1}\tag{2}$$

The graphical representation of (2) is as follows :

On this figure, one can observe

• the presence of a horizontal asymptote attesting that the closest distance $d$ is to $4=1+2+1$ (extreme case where circles $C_1,C_2,C_3$ are in a row giving the degenerate cases of a circle $C_4$ with infinite radius), the largest is the value or $r$,

• on the left, the stopping point (little red point) with coordinates $(2 \tfrac{\sqrt{3}}{3}-1,2)$ corresponds to another extreme case : the configuration were $C_1,C_2,C_3$ are mutually tangent.

SAGE program :

 var('r1 r2 r3 r4 d')
 r1=1
 r2=1
 r3=1
 CM=matrix([
 [0,1,1,1,1],
 [1,0,(r1+r2)^2,d^2,(r1+r4)^2],
 [1,(r1+r2)^2,0,(r2+r3)^2,(r2+r4)^2],
 [1,d^2,(r2+r3)^2,0,(r3+r4)^2],
 [1,(r1+r4)^2,(r2+r4)^2,(r3+r4)^2,0]])
 show(CM)
 dCM=expand(CM.det())
 print(dCM)
 s=solve(dCM,d,multiplicities=False) # explicit expression d=f(r4)
 print(s[1])
 g=implicit_plot(dCM,(r4,0,4),(d,0,5))
 show(g)