Is there a unified equation for ellipses, parabolas, and hyperbolas in cartesian coordinates with eccentricity as a parameter?

Question

In polar coordinates, we can represent a conic of arbitrary eccentricity, be it a ellipse, parabola, or hyperbola, as $$r = \frac{1}{1+\varepsilon \cos \theta}.$$ This equation has the eccentricity as an explicit parameter.

In Cartesian coordinates, we normally use separate equations for parabolas. We are "forced" to do this, because the standard equations fix the center of the ellipse and hyperbola at the origin, and parabolas have no center. (The polar equation above avoids this, because the center is not fixed at the origin.)

Of course, as Intelligenti pauca points out, there is the general second degree equation - but this hides the eccentricity.

It should be possible to do something similar in Cartesian coordinates: Come up with a single equation which can, based on a parameter showing the eccentricity, represent an ellipse, parabola, or hyperbola, by allowing the center to float (or go to infinity). I even think I came across such an equation once, but can find no record. Is there such an equation?

Answer 1

Your polar equation assumes a semi-latus rectum $l$ equal to 1. You can extend this to be more general $$r = \frac{l}{1+\epsilon\cos\theta}$$

The latus rectum is the chord of the conic section paralel to the directrix and passing through the focus. $l$ is defined as half of its length, which is the same as $d\epsilon$, where $d$ is the distance between the focus and the directrix. So (more generally) the equation can be written as $$r = \frac{d\epsilon}{1+\epsilon\cos\theta}$$

Then all that is left is to rearrange and convert to cartesian coordinates. I'll skip out some sections, but first it will help to rearrange in terms of $\epsilon$ $$\epsilon = \frac{r}{d - r\cos\theta}$$

After squaring, plugging in $r^2=x^2+y^2$ and $r\cos\theta=x$ and collecting like terms you're left with $$x^2 + \frac{2d\epsilon^2}{1-\epsilon^2}x + \frac{y^2}{1-\epsilon^2} = \frac{d^2\epsilon^2}{1-\epsilon^2}$$

You can then complete the square and do a final rearrangement for the "constant" term to get $$\left(x + \frac{d\epsilon^2}{1-\epsilon^2}\right)^2 + \frac{y^2}{1-\epsilon^2} = \frac{d^2\epsilon^2}{(1-\epsilon^2)^2}$$

Hopefully you can see this looks like a conic section. You could "normalise" this expression by dividing by the RHS to give something equal to 1, but it's messy and isn't necessary. Notice that when $\epsilon<1$ the coefficient of $y^2$ is positive, and when $\epsilon>1$ the coefficient is negative, which is what we expect from the general forms of the ellipse and the hyperbola. Note that the equation is invalid for $\epsilon=1$ (parabola)

Edit: as an additional remark, my original equaiton for $r$ can instead be written with a $-\epsilon\cos\theta$; this switches which of the foci we are working with and produces a final equation with $x-\dots$ instead of $x+\dots$, which just reflects the graph in the $y$ axis. Similarly, one can use $\sin$ instead of $\cos$, when there is a horizonal directrix - this produces a final equation with the $x$ and $y$ swapped

Answer 2

Starting with your polar equation

$$r = \frac{1}{1+\varepsilon \cos \theta}$$

Substitute $\cos\theta = \frac{x}{r}$, to get:

$$r = \frac{1}{1+\varepsilon x/r}$$

Solve for $r$ to get:

$$r = 1 - \varepsilon x$$ $$\sqrt{x^2 + y^2} = 1 - \varepsilon x$$ $$x^2 + y^2 = 1 - 2\varepsilon x + \varepsilon^2 x^2$$ $$\boxed{(1 - \varepsilon^2)x^2 + 2\varepsilon x + y^2 = 1}$$

Or if $\varepsilon \ne 1$:

$$\boxed{\left(x + \frac{\varepsilon}{1 - \varepsilon^2}\right)^2 + \frac{y^2}{1 - \varepsilon^2} = \frac{1}{(1 - \varepsilon^2)^2}}$$

If $\varepsilon = 0$, the equation reduces to $x^2 + y^2 = 1$, the standard unit circle.

If $0 < \varepsilon < 1$, we get an ellipse, e.g., $\varepsilon = \frac{1}{2} \implies \frac{9}{16}\left(x + \frac{2}{3}\right)^2 + \frac{3}{4}y^2 = 1$.

If $\varepsilon = 1$, the equation reduces to $y^2 = 1 - 2x$, a parabola with its vertex at $(\frac{1}{2}, 0)$, opening to the right.

If $\varepsilon > 1$, we get a hyperbola, e.g., $\varepsilon = 2 \implies 9\left(x - \frac{2}{3}\right)^2 - 3y^2 = 1$.

As $\varepsilon \to \infty$, the equation degenerates into the straight line $x = 0$.

Answer 3

Too long for a comment:

Dan's answer and M.Riyan's comment could both be rearranged to $$y=\pm\sqrt{ (1-\varepsilon x)^2-x^2}$$

which if plotted would give the same results as your $r = \frac{1}{1+\varepsilon \cos \theta}$, as below with a circle $\varepsilon =0$ in black, an ellipse $\varepsilon =\frac12$ in grey, a parabola $\varepsilon =1$ in red, and two hyperbolae $\varepsilon =2$ in blue and $\varepsilon =4$ in cyan.

Note that all your curves pass through $(x,y)=(0,\pm1)$ corresponding to $(r,\theta)=(1,\pm\frac\pi2)$ in your polar equation, and that each passes through $(x,y)=(\frac1{1+\varepsilon},0)$ corresponding to $(r,\theta)=(\frac1{1+\varepsilon},0)$ in your polar equation, and (if it exists) through $(x,y)=(-\frac1{1-\varepsilon},0)$ corresponding to $(r,\theta)=(\frac1{1-\varepsilon},\pm \pi)$ in your polar equation.

Answer 4

I find this form useful ...

---

The equation for a (non-circle) conic is, abstractly, $$\text{distance to focus} \;=\;\text{eccentricity} \cdot ( \text{distance to directrix} ) \tag1$$ (The problem with a (non-point) circle is that the its directrix lies at infinity. Ultimately, this issue shakes itself out.)

In particular, consider a (non-circle) conic with eccentricity $e>0$, focus $F:=(f_x,f_y)$, semi-latus rectum $r$ (and thus focus-to-directrix distance $r/e$), and focus-to-vertex direction vector $v:=(\cos\theta,\sin\theta)$. The conic's axis meets the directrix at $D:=F+\frac{r}{e}v$, so the directrix has this equation (beginning with its point-normal form): $$\begin{align} 0 &= v\cdot\left((x,y)-D\right) \\ &=v\cdot(x-f_x,y-f_y)-\frac{r}{e}|v|^2 \\ &=(x-f_x)\cos\theta+(y-f_y)\sin\theta-\frac{r}{e} \end{align}$$ Thus, invoking the formulas for the distance between two points and the distance from a point to a line, $(1)$ becomes $$\begin{align} \sqrt{(x-f_x)^2+(y-f_y)^2} &= e\;\frac{\left|\;(x-f_x)\cos\theta+(y-f_y)\sin\theta-\dfrac{r}{e}\;\right|}{\sqrt{\cos^2\theta+\sin^2\theta}} \\[4pt] &= \left|\;(x-f_x)\,e\cos\theta+(y-f_y)\,e\sin\theta-r\;\right| \tag{1'} \end{align}$$ Squaring, we obtain this form: $$(x-f_x)^2+(y-f_y)^2 \;=\; \left(\; (x-f_x)\,e\cos\theta+(y-f_y)\,e\sin\theta-r \;\right)^2 \tag2$$ (Suddenly, $e=0$ is no longer a problem, so I can drop the "non-circle" disclaimer.) Expanding and collecting terms (and multiplying by an arbitrary constant $k$), we see the defining geometric elements of the conic encoded in the coefficients of the general second-degree polynomial, thusly: $$K(x,y) \;=\; k_{20}x^2 + 2k_{11}xy + k_{02}y^2 + 2 k_{10}x+2k_{01} y + k_{00}$$ $$\begin{align} k_{20} &:= \phantom{-}k\left(1-e^2\cos^2\theta \right) \\ k_{02} &:= \phantom{-}k\left(1-e^2\sin^2\theta \right) \\ k_{11} &:= -k\,e^2\sin\theta\cos\theta \\ k_{10} &:= \phantom{-}k e r \cos\theta - k_{20}f_x - k_{11}f_y \\ k_{01} &:= \phantom{-}k e r \sin\theta - k_{11}f_x - k_{02}f_y \\ k_{00} &:= -k r^2 - k_{20}f_x^2 - k_{02}f_y^2 - 2 k_{11}f_x f_y - 2 k_{10}f_x - 2 k_{01}f_y \end{align}$$

The $k$ is there because multiplying the polynomial through by a non-zero constant doesn't change the conic; so, if someone hands you a polynomial associated with a conic, you can't assume that it exactly matches $(2)$.

---

Teasing the geometric parameters out of the polynomial coefficients is really beyond the scope of this answer, but I'll note a few interesting relations: $$M := \begin{bmatrix} k_{20} & k_{11} & k_{10} \\ k_{11} & k_{02} & k_{01} \\ k_{10} & k_{01} & k_{00} \end{bmatrix} \qquad M_{00} := \begin{bmatrix} k_{20} & k_{11} \\ k_{11} & k_{02} \end{bmatrix}$$ $$\begin{align} m &:= \det M &&=-k^3 r^2 \\ \sigma &:= \operatorname{sgn} m && = -\operatorname{sgn}k \\[8pt] m_{00} &:= \det M_{00} = k_{20}k_{02}-k_{11}^2 &&= \phantom{-}k^2 \left(1-e^2\right)\\[8pt] p &:= k_{20}+k_{02} &&= \phantom{-}k\left(2-e^2\right) \\ q &:= \sqrt{(k_{20}-k_{02})^2+4k_{11}^2} && = |k|e^2 = -\sigma k e^2 \end{align} \tag4$$ With the above, we find $$\begin{align} (k-k_{20})(k-k_{02}) &= k_{11}^2 \tag5 \\[4pt] (1 - e^2) q^2 &= e^4 m_{00} \tag6 \\[4pt] (k_{20} - k_{02})\sin2\theta &= 2k_{11} \cos2\theta \tag7 \end{align} $$ Note that $(5)$ marks $k$ as an eigenvalue of $M_{00}$. (What's the corresponding eigenvector?) Sign $\sigma$ helps us identify which of the two eigenvalues is $k$. This, in turn, allows us to calculate $r^2$:
$$ k = \frac12\left(p - \sigma q\right) \qquad\qquad r^2 = -\frac{m}{k^3} \tag8 $$ I'll stop here.

Answer 5

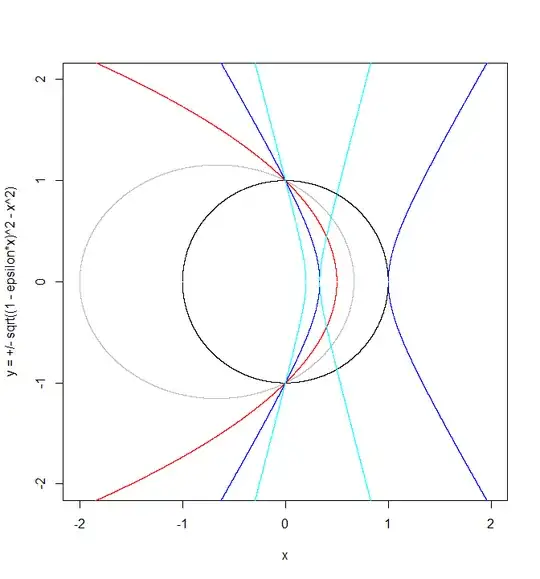
Posting a second answer with a different approach: Let's start with the equation of an ellipse centered at $(x_0, y_0)$.

$$\left(\frac{x - x_0}{a}\right)^2 + \left(\frac{y - y_0}{b}\right)^2 = 1$$

Or equivalently:

$$b^2x^2 + a^2y^2 - 2b^2x_0x - 2a^2y_0y + (b^2x_0^2 + a^2y_0^2 - a^2b^2) = 0$$

But this doesn't quite match up to the generic conic form $Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$ because the $Bxy$ term is missing. So let's introduce an alternate coordinate system $(x', y')$ that doesn't require the $xy$ term.

$$A'x'^2 + C'y'^2 + D'x' + E'y' + F' = 0$$

Let $x = r\cos\theta$ and $y = r\sin\theta$. But rotate the coordinate system so that

$$x' = r\cos(\theta + \phi) = r(\cos\theta\cos\phi - \sin\theta\sin\phi) = x\cos\phi - y\sin\phi$$ $$y' = r\sin(\theta + \phi) = r(\sin\theta\cos\phi + \cos\theta\sin\phi) = y\cos\phi + x\sin\phi$$

Substituting into the alternate coordinate equation gives:

$$A'(x\cos\phi - y\sin\phi)^2 + C'(y\cos\phi + x\sin\phi)^2 + D'(x\cos\phi - y\sin\phi) + E'(y\cos\phi + x\sin\phi) + F' = 0$$

which expands to:

$$(A'\cos^2\phi + C'\sin^2\phi)x^2 + 2(C' - A')\cos\phi\sin\phi xy + (A'\sin^2\phi + C'\cos^2\phi)y^2 + (D'\cos\phi + E'\sin\phi)x + (E'\cos\phi - D'\sin\phi) + F' = 0$$

Plugging in the coefficients from the $xy$-less ellipse equation gives:

$$A = b^2\cos^2\phi + a^2\sin^2\phi$$ $$B = 2(a^2 - b^2)\cos\phi\sin\phi$$ $$C = b^2\sin^2\phi + a^2\cos^2\phi$$ $$D = -2b^2\cos\phi - 2a^2\sin\phi$$ $$E = -2a^2\cos\phi + 2b^2\sin\phi$$ $$F = b^2x_0^2 + a^2y_0^2 - a^2b^2$$

We can derive from these that $A + C = a^2 + b^2$ and $B^2 - 4AC = -4a^2b^2$.

Define the aspect ratio ($R$) of an ellipse as the quotient $\frac{a}{b}$. Or should that be $\frac{b}{a}$? The two values are just reciprocals of each other. Instead of choosing, let's add them.

$$R + \frac{1}{R} = \frac{a}{b} + \frac{b}{a} = \frac{b}{a} + \frac{a}{b}$$ $$\frac{R^2 + 1}{R} = \frac{a^2 + b^2}{ab}$$

But making the substitutions $a^2 + b^2 = A + C$ and $a^2b^2 = \frac{B^2 - 4AC}{-4}$ and rearranging into a polynomial in $R$ gives:

$$(B^2 - 4AC)R^4 + (4A^2 + 2B^2 + 4C^2)R^2 + B^2 - 4AC = 0$$

Applying the Quadratic Formula to solve for $R^2$ gives:

$$\boxed{R^2 = \frac{-(2A^2 + B^2 + 2C^2) \pm 2 (A + C)\sqrt{(A - C)^2 + B^2}}{B^2 - 4AC}}$$

Note that as the curve approaches a parabola ($B^2 - 4AC \to 0$), we get a division by zero, and thus an “infinite” aspect ratio. And if $B = 0$, the above formula simplifies to $R^2 \in \{ \frac{A}{C}, \frac{C}{A} \}$. And for a circle, we simply have $R^2 = 1$.

Now, let's find how aspect ratio is related to eccentricity. By plugging in the coefficients from my previous answer, we get:

$$R^2 \in \{ 1 - \varepsilon^2, \frac{1}{1 - \varepsilon^2} \}$$ $$\varepsilon = \pm\sqrt{1 - R^2} \text{ or } \varepsilon = \pm{\sqrt{1 - \frac{1}{R^2}}}$$

But $\varepsilon$ should be a positive real number, so this gives:

$$\boxed{\varepsilon = \begin{cases} \sqrt{1 - R^2} & \text{if } R^2 \le 1 \\ \sqrt{1 - \frac{1}{R^2}} & \text{if } R^2 \ge 1 \end{cases}}$$

By allowing the aspect ratio $R$ to be either real or imaginary, we can have this formula accommodate all types of conic sections:

• Circle: $R^2 = 1$, $\varepsilon = 0$
• Ellipse: $R^2 > 0$, $0 \le \varepsilon < 1$
• Parabola: $R^2 = 0 \lor R^2 = \infty$, $\varepsilon = 1$
• Hyperbola: $R^2 < 0$, $\varepsilon > 1$

Answer 6

It is insightful to retain the latus-rectum $p$ also along with eccentricity. Newton's polar formula contains two essential constants $(p,\epsilon)$ so it is best not to have a unit semi latus rectum and exclude it. Newton did include them both.

Converting Newton's Conics form ( that has eccentricity $\epsilon $ and semi-latus rectum with focus as origin ) to Cartesian coordinates $$ \frac{p}{r}=1 + \epsilon \cos \theta $$ $$ p= r+ \epsilon x = \sqrt{x^2+y^2}+ \epsilon x $$ Simplifying

$$ \boxed{y^2=x^2(\epsilon^2-1)-2 p\epsilon ~x +p^2} $$

Here $\epsilon >1$ for a hyperbola, $\epsilon <1$ for an ellipse.

For $\epsilon=0$ we have the circle radius $R$ $$ x^2+y^2=p^2 = R^2 $$ For $\epsilon=1$ we have the parabola $$ y^2=p^2 -2 px $$ If $p= 2f$ for a parabola where $f$ is focal length $$ y^2= 4f(f-x) $$

Substitutions $$ x\to x+h, y\to y+k $$

transform the focal form to conics with axes parallel to coordinate axes.