The radius of a circle is equal to the distance between the focal points of the parabolas only if the two directrices are perpendicular

Question

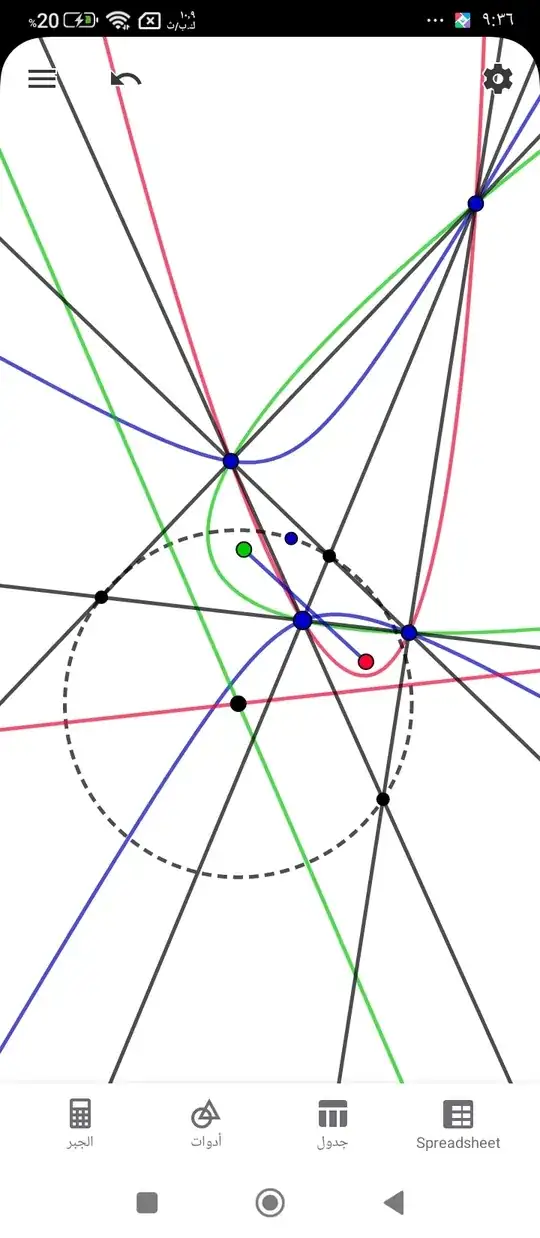
Today I came up with many beautiful results in parabola, but I decided to present the most prominent result in the form of a question on this site, I think it is a really special feature

Let's have two parabolas intersecting in four points, these four points form the vertices of a convex quadrilateral, if we draw all the straight lines connecting these four points, we get three additional intersection points, now we draw the circle passing through these three points, this property says that the radius of this circle is equal to the distance between the foci of the parabolas if and only if the guides of the parabolas are perpendicular, or in other words, it happens if and only the intersection of the parabolas at four points located On one circle, is there anyone who can prove it? And is this property known in advance? Please provide any references on the subject

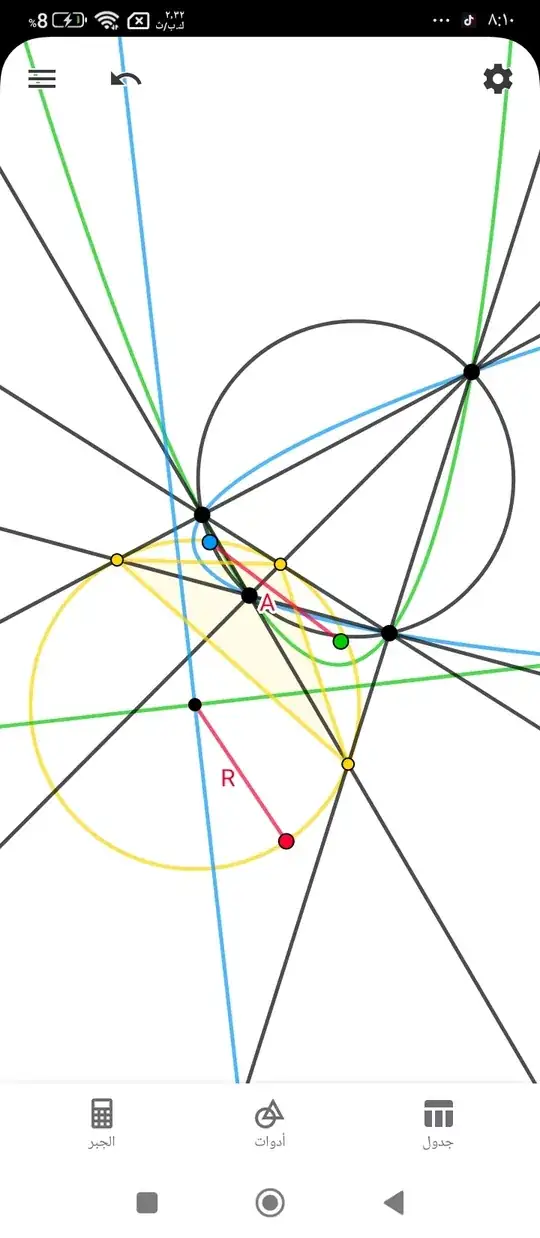
Given: $P$ is a parabola with focus $F_p$ and directrix $\Delta_p$, and $Q$ is a parabola with focus $F_q$ and directrix $\Delta_q$. Let $P \cap Q = { A, B, C, D }$, $\Delta_p \cap \Delta_q = O$, $\overline{AB} \cap \overline{CD} = U$, $\overline{AC} \cap \overline{BD} = V$, and $\overline{AD} \cap \overline{BC} = W$. Let $G$ be the circle passing through points $U$, $V$, and $W$ with a radius $R$.

Requirement 1: Prove that $O$ is the center of $G$.

Requirement 2: Prove that $\Delta_p \perp \Delta_q \iff \overline{F_p F_q} = R$.

edit: I have finally arrived at the general case of the theorem. We no longer need the orthogonality of the two equivalent segments' directions to find the relationship between $A$ and $R$. There is a simple and elegant algebraic relationship given by $A = R \times \sin(\theta)$, where $\theta$ represents the angle measure between the directions of the two equivalent segments.

New edit: I just discovered a new property related to shape that may be useful in finding a geometric proof

There is a single hyperbola with two perpendicular approaches that passes through the four points where the two parabolas intersect, the center of this hyperbola belongs to the circle we used to explain this theorem

Answer 1

$$ \newcommand{\cis}{\operatorname{cis}} \newcommand{\ww}{\omega} \newcommand{\cww}{\overline{\omega}} \newcommand{\ss}{\sigma\,} $$ Let's start with a convex quadrilateral and determine the circumscribing parabolas from there. The complex plane will make some coordinate representations cleaner.

Let the diagonals of $\square ABCD$ meet at the origin such that the angles they form are bisected by the coordinate axes. For (real) positive $a$, $b$, $c$, $d$, and $0<\theta<\pi/2$, assign complex coordinates as follows: $$\ww:=\cos\theta+i\sin\theta \qquad \cww=\frac1\ww = \cos\theta-i\sin\theta$$ $$ A = \frac{\;\ww\;}{a} \quad B = \frac{\;\cww\;}{b} \quad C =-\frac{\;\ww\;}{c} \quad D =-\frac{\;\cww\;}{d}$$

Define $P:=AD\cap BC$ and $Q:=AB\cap CD$, and let $R$ be the center of $\bigcirc OPQ$. We find, without too much trouble, $$\begin{align} P &= \phantom{-}\frac{(a+c)\,\cww + (b+d)\,\ww}{a b - c d } \tag1\\[4pt] Q &= - \frac{(a + c)\,\cww - (b + d)\,\ww }{ad-bc} \tag2\\[4pt] R &= \;i\; \frac{ \left((a+c)^2\,\cww^2-(b + d)^2\,\ww^2\right) \left((a - c)\,\ww - (b - d)\,\cww)\right)}{4\sin2\theta\,(a b - c d) (a d - b c) } \tag3 \end{align}$$

Now, the two circumparabolas of $\square ABCD$ have (usual Cartesian) equations of the form $$K_\pm\;:\; k_{20} x^2 + 2k_{11} xy+ k_{02}y^2+2k_{10}x+2k_{01}y+k_{00}=0$$ where, for $\sigma = \pm1$ matching the subscript of $K_\pm$, and $a_2:=\sqrt{a}$, etc, the coefficients are $$\begin{align} k_{20} &= u^2 \quad k_{02} = v^2 \quad k_{11} = uv & u &:= (a_2 c_2 -\ss b_2 d_2) \sin\theta \\ && v &:= (a_2 c_2 +\ss b_2 d_2) \cos\theta \\ k_{10} &= ((a-c)+(b-d)) \cos\theta \sin^2\theta \\ k_{01} &= ((a-c)-(b-d)) \cos^2\theta \sin\theta \\ k_{00} &= -\sin^2 2\theta \end{align} \tag4$$ The parabola's axis has direction vector $(v,u)$ (or its opposite, but that counts), so that the two axes (as well as the parabolas' directrices) make an angle $\psi$ satisfying $$\sin\psi \;=\; \frac{u_+ v_- -\, v_+ u_-}{\sqrt{(u_+^2+v_+^2)(u_-^2+v_-^2)}} \;=\; \frac{2 a_2 b_2 c_2 d_2 \sin2\theta}{\sqrt{a^2 c^2 + b^2 d^2 - 2 a b c d \cos4\theta}} = \frac{2a_2b_2c_2d_2\sin2\theta}{\left|a c\cww^2 - b d \ww^2\right|} \tag5$$ The parabola's focus is $$F = \frac{ \left((a_2\cww + \ss b_2\ww)^2 + (c_2\cww - d_2\ww)^2\right) \left((a_2\cww - \ss b_2\ww)^2 + (c_2\cww + d_2\ww)^2\right)}{ 4\sigma (a_2 b_2 - \ss c_2 d_2)(a_2 d_2 + \ss b_2 c_2) \left(a_2 c_2\cww^2 + \ss b_2 d_2 \ww^2\right)} \tag6$$ and we find $$\frac{F_+-F_-}{R} = -i\;\underbrace{\frac{(a - c)\cww - (b - d) \ww}{(a - c)\ww - (b - d)\cww}}_{\text{ratio of conjugates, so norm $1$}}\;\;\frac{2 a_2 b_2 c_2 d_2 \sin2\theta}{a c\cww^2 - b d \ww^2} \tag7$$ whence $$|F_+-F_-| = |R|\sin\psi \tag8$$ This confirms OP's claim. $\square$

---

Note. While gleaning a general conic's geometric characteristics from its algebraic equation can be messy (see this recent answer, the burden lifts considerably for a parabola ...

Defining $k := \sqrt{k_{20}+k_{02}}$, the semi-latus rectum $r$ is given by $$r^2 = -\frac{1}{k^3} \left|\begin{matrix} k_{20} & k_{11} & k_{10} \\ k_{11} & k_{02} & k_{01} \\ k_{10} & k_{01} & k_{00} \end{matrix}\right|$$ The focus-to-directrix vector $(r\cos\phi,r\sin\phi)$, and the coordinates of the focus $(f_x,f_y)$ are given by these relations:

$$\begin{align} k_{02}k_{10} - k_{11}k_{01} &= k^2 r\cos\theta \\ k_{20}k_{01} - k_{11}k_{10} &= k^2 r\sin\theta \\ k_{01}^2 - k_{02}k_{00} &= k^2 \left( 2 f_x\,r\cos\theta + r^2 \right) \\ k_{10}^2 - k_{20}k_{00} &= k^2 \left( 2 f_y\,r\sin\theta + r^2 \right) \end{align}$$

(Note that the left-hand sides are determinants of sub-matrices of the $3\times 3$ matrix used to calculate $r^2$.)

Answer 2

It looks rather natural to apply analytical geometry to find the answer and this my quest is in progress. Below I present my current advances.

Let us introduce the coordinates at the plane such that $O$ is the origin, $\Delta_p$ is the $Ox$ axis and $\alpha$ is the angle between $\Delta_q$ and $\Delta_q$. Then the equations of the parabolas $P$ and $Q$ are $$x^2=f_p(2y-f_p)$$ and $$(x\cos\alpha+y\sin\alpha)^2=f_q(-2x\sin\alpha+2y\cos\alpha-f_q),$$ respectively, where $f_p$ and $f_q$ are the focal parameters of $P$ and $Q$, respectively. Moreover, the foci $F_p$ and $F_q$ have the coordinates $(0,f_p)$ and $(-f_q\sin\alpha,f_q\cos\alpha)$, respectively. Then the coordinates $(x_A,y_A)$,$(x_B,y_B)$,$(x_C,y_C)$, and $(x_D,y_D)$, of the points $A$,$B$, $C$, and $D$, respectively, are the solutions of the system $$\begin{cases} x^2=f_p(2y-f_p)\\ (x\cos\alpha+y\sin\alpha)^2=f_q(-2x\sin\alpha+2y\cos\alpha-f_q). \end{cases} $$

Note that the first equation implies that $x_A$, $x_B$, $x_C$, and $x_D$ are pairwise distinct.

Let $(x_U,y_U)$ be the coordinates of the point $U$. Then $$\left|\begin{matrix} x_A & y_A & 1\\ x_B & y_B & 1\\ x_U & y_U & 1 \end{matrix}\right| =0= \left|\begin{matrix} x_C & y_C & 1\\ x_D & y_D & 1\\ x_U & y_U & 1 \end{matrix}\right|.$$

Expanding the first equality, we obtain

$$x_U(y_A-y_B)+y_U(x_B-x_A)+x_Ay_B-x_By_A=0$$

Substituting $y_A=\frac 12\left(\frac {x_A^2}f_p+f_p\right)$ and $y_B=\frac 12\left(\frac {x_B^2}f_p+f_p\right)$ and then dividing by $x_A-x_B$, we obtain

$$x_U(x_A+x_B)-2f_py_U+2f_p^2-x_Ax_B=0.$$

Similarly we obtain

$$x_U(x_C+x_D)-2f_py_U+2f_p^2-x_Cx_D=0.$$

So $x_U(x_A+x_B-x_C-x_D)=x_Ax_B-x_Cx_D$.

The equations for the coordinates of the points $V$ and $W$ are similar. We have to show that $$x_U^2+y_U^2=x_V^2+y_V^2=x_W^2+y_W^2.$$ Moreover, if $R^2$ is the latter quantity then we have to show that $$R^2=|F_pF_q|^2=f_q^2\sin^2\alpha+(f_q\cos\alpha-f_p)^2\Leftrightarrow \alpha=\pm? \pi/2.$$