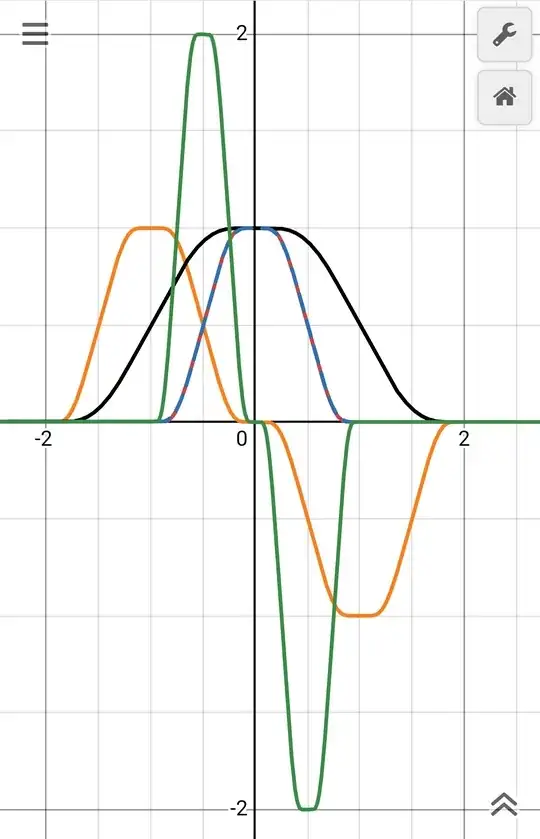
I am trying to build a function $q(x)$ from another function $f(x)$ as:
- $g(x)=f(x+1)-f(x-1)$
- $z(x)=\int\limits_{-2}^{x} g(u)\ du$
- $q(x)=z(2x)$
from the function I took from here:
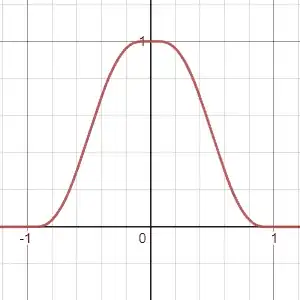
$$f(x) = \begin{cases} 0,\quad x\leq -1\\ 0,\quad x\geq 1\\ 1,\quad x=0\\ \dfrac{1}{1+\exp\left(\frac{1-2|x|}{x^2-|x|}\right)},\quad\text{otherwise} \end{cases}$$
but I got stuck finding the integral of point 2 in Wolfram-Alpha.
Do you believe it would be possible to find $q(x)$ in closed form?
You could see the plots of the functions in Desmos, but it takes a while to load (I don't know why).
Motivation
I am trying to make a smooth bump function with straight line edges on their slopes, like the ones the Rvachëv function $R(x)$ has, which is made by the first lobe of the Fabius function $F(x)$ centered at cero:
$$R(x)=\begin{cases}0,\, |x|\geq 1\\ F(x+1),\,|x| <1\end{cases}$$
This function show to have a flat top, and it could be seen it do have straight line edges on its slope from the Delay differential equation it solves $R'(x) = 2R(2x+1)-2R(2x-1)$.
$f(x)$ already looks very close to $R(x)$ as you could see from the polynomial approximation shown here, but their edges are not straight lines in a rigorous sense.
Update 1
Thanks to the comment by @mattTheMathLearner I think I could summarize the problem into finding the primitive to:
$$u(x) = \begin{cases} 0,\quad |x|\geq 1\\ 0,\quad x= 0\\ 2,\quad x=-\frac12\\ -2,\quad x=\frac12\\ \dfrac{-2\,\text{sgn}(x)}{1+\exp\left(\frac{1-2||2x|-1|}{(|2x|-1)^2-||2x|-1|}\right)},\quad\text{otherwise} \end{cases}$$
then what I am trying to figure out is the close form of:
$$q(x)=\int\limits_{-1}^{x}u(y)dy$$
Here their look in Desmos (takes a wild to load).
Update 2
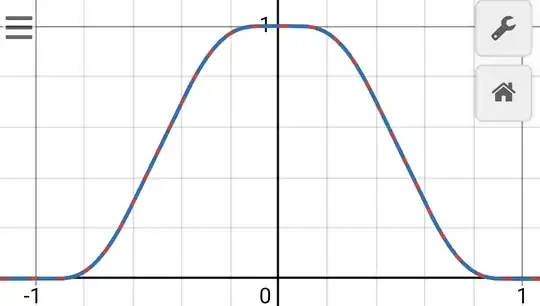
I compared in Desmos $q(x)$ with an approximation of the Rvachëv function and they look really close.
Could someone review if $q(x)$ actually is an exact formulation of the Rvachëv function as shown here? (it shouldn't be, but it get so closed it get suspicious)
Forget Update 2: I check in Desmos and it don't fulfill exactly the Rvachëv function delayed differential equation, but it was very close indeed, kinda cool.
Update 3
I realized later I could make a family of bump functions: $$q(x,k)=\int\limits_{-1}^{x}u(y,k)dy$$
and
$$u(x,k) = \begin{cases} 0,\quad |x|\geq 1\\ 0,\quad x= 0\\ 2,\quad x=-\frac12\\ -2,\quad x=\frac12\\ \dfrac{-2\,\text{sgn}(x)}{1+\exp\left(\frac{k(1-2||2x|-1|)}{(|2x|-1)^2-||2x|-1|}\right)},\quad\text{otherwise} \end{cases}$$
which kinda looks like "bumps" for $k\geq\frac{\sqrt{3}}{2}$. Also when $k\to\infty$ the function $q(x,k)$ becomes a truncated pyramid.