Finding the metallic ratio $4+\sqrt{17}$ in the diagonals of the $17$-gon?

Question

(Note: All images except the $13$-gon are from Antonia Buitrago's 2007 article "Polygons, Diagonals, and the Bronze Mean".)

I. The golden ratio

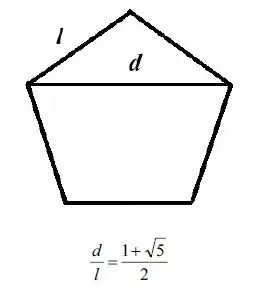
We are familiar with how $\phi$ appears in the regular pentagon,

If the pentagon has unit length $l=1$, then diagonal $d=\frac{1+\sqrt{5}}2.$ But $\phi$ is just the first metallic ratio, or the quadratic root $R_m$,

$$R_m = \frac{m+\sqrt{m^2+4}}2$$

the next is the silver ratio $R_2 = \frac{2+\sqrt{8}}2 = \small{1+\sqrt{2}}\, ,$ the bronze ratio $R_3 = \frac{3+\sqrt{13}}2$, and so on.

Proposal: We generalize the pentagonal case: Using more than one diagonal of a polygon, can we express all $R_m$? It seems the answer is yes.

---

II. Diagonals

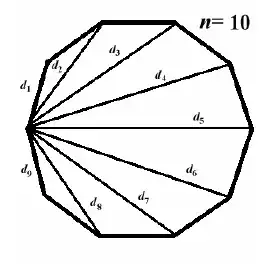
Given a regular polygon, we follow Buitrago and define a particular set of diagonals $d_k$ as "the line segments joining a common vertex $v_0$ to vertex $v_k$". For example,

Hence $d_1$ is from $v_0$ to $v_1$, while $d_2$ is from $v_0$ to $v_2$, and so on. And $d_1 = d_9$ is just the side length of the decagon. The ratio of $d_k$ to $d_1$ is given by,

$$\frac{d_k}{d_1} = \frac{\sin\frac{k\,\pi}n}{\sin\frac{\pi}n} = \sqrt{\frac{1-\cos\frac{2k\pi}n}{1-\cos\frac{2\pi}n}}$$

For the regular $n$-gon with unit side length $d_1 = 1$, define these diagonals as,

$$D_n(k) = \frac{\sin\frac{k\,\pi}{n}}{\sin\frac{\pi}{n}}\qquad\qquad$$

---

III. Data

$$\small{\begin{align} \phi=\frac{1+\sqrt{5}}2\; &= D_5(2)\\ 1+\sqrt{2}=\frac{2+\sqrt{8}}2\; &= D_4(1)+D_4(2) \,=\, D_8(3)\\ U_{13}=\frac{3+\sqrt{13}}2 &= \color{blue}1D_{13}(1)+D_{13}(3)+D_{13}(4)-D_{13}(5)\\ \phi^3=\frac{4+\sqrt{20}}2 &= D_{5}(1)+D_{5}(2)+D_{5}(3) \,=\, D_{10}(1)+D_{10}(5)\\ U_{29} = \frac{5+\sqrt{29}}2 &= \color{blue}2D_{29}(1)+D_{29}(2)+D_{29}(3)-D_{29}(4)-D_{29}(7)+\dots+D_{29}(14)\\ 3+\sqrt{10}=\frac{6+\sqrt{40}}2 &= 3D_{20}(1)+D_{20}(4)+D_{20}(6)-2D_{20}(8)+D_{20}(10)\\ U_{53}=\frac{7+\sqrt{53}}2 &= \color{blue}3D_{53}(1)+D_{53}(2)+D_{53}(3)-D_{53}(6)-D_{53}(7)+\dots+D_{53}(26)\\ 4+\sqrt{17}=\frac{8+\sqrt{68}}2 &= 3D_{17}(1)-2D_{17}(2)+2D_{17}(5)-2D_{17}(7)+2D_{17}(8) \end{align}}$$

and so on, where $U_n$ is a fundamental unit. It seems it is easy to predict the coefficient of $D_n(1)$ when $n=m^2+4$ is prime. (Curiously, I couldn't find $3+\sqrt{10}$ in the decagon. I had to use the $20$-gon.)

---

IV. The 13-gon

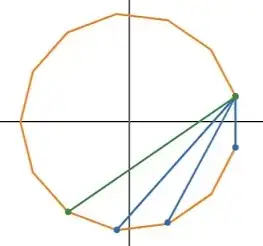
A picture is worth a thousand words. Assume a $13$-gon with unit side length,

Let the common vertex be $v_0$ which connects to vertices $v_1, v_3, v_4, v_5$. Then the sum of the three blue lines minus the green line is the bronze ratio,

$$\left(\frac{\sin\frac{1\pi}{13}}{\sin\frac{\pi}{13}}\right)+\left(\frac{\sin\frac{3\pi}{13}}{\sin\frac{\pi}{13}}\right)+\left(\frac{\sin\frac{4\pi}{13}}{\sin\frac{\pi}{13}}\right)-\left(\frac{\sin\frac{5\pi}{13}}{\sin\frac{\pi}{13}}\right)= \frac{3+\sqrt{13}}2$$

Or in the notation of the previous sections,

$$D(1)+D(3)+D(4)-D(5) = \frac{3+\sqrt{13}}2$$

where $D(k)=D_{13}(k)$ and the subscript has been suppressed for brevity. Image is courtesy of the Desmos Polygon Calculator.

---

V. Question

What is the general formula to express the metallic ratios,

$$R_m = \frac{m+\sqrt{m^2+4}}2$$

in terms of these diagonals $D_n(k)$, especially if $n=m^2+4$ is prime?

For example, since $D_n(1)=1$, how do we generate the next $\frac{13-1}4=3$ numbers $k=(3, 4, 5)$, or $\frac{17-1}4=4$ numbers $k=(2, 5, 7, 8)$, or $\frac{29-1}4=7$ numbers $k=(2, 3, 4, 7, 10, 12, 14)$ from first principles?

Answer 1

For the case where the number $m^2+4$ inside the square root (the discriminant) is a prime $p$ or four times a prime ($4p$), we can get the appropriate combinations using quadratic Gauss sums. If $p$ is any odd prime then we have the following:

$\sum\limits_{r=1}^{p-1}(r|p)\exp(2\pi ri/p)=\epsilon\sqrt{p},$

where $(r|p)$ is the Legendre symbol of residue $r\bmod p$ and $\epsilon$ is $1$ for a prime one greater than a multiple of $4$, or $i$ for a prime one less than a multiple of $4$. The Legendre symbol is one of the following:

• $+1$ if $r$ is the square of some nonzero residue $\bmod p$

• $0$ for $r=0$ (not needed in this problem)

• $-1$ otherwise

Only primes one greater than a multiple of $4$ are in scope, so we render $\epsilon=1$ and take the real part of the above identity. For such primes the additive-inverse residues $r$ and $p-r$ will have the same Legendre symbol. We then have

$2\sum\limits_{r=1}^{(p-1)/2}(r|p)\cos(2\pi r/p)=\sqrt{p},\tag{1}$

which will be our starting point for the derivation.

Let us work things out for $p=13$. To simplify the presentation tbe following are defined:

$c_k=\cos(2\pi k/p)=\cos(2\pi k/13)$

$c_k=\sin(2\pi k/p)=\sin(2\pi k/13)$

where $2k\in\mathbb{Z}.$ It will be convenient to allow half-integer values for $k$.

Modulo $13$, the Legendre symbols for residues $1$ through $6$ are respectively $+1,-1,+1,+1,-1,-1$ and therefore (1) becomes

$2(c_1-c_2+c_3+c_4-c_5-c_6)=\sqrt{13}\tag{2}$

Our first move is to multiply tbis by $s_{1/2}=\sin(\pi/p)=\sin(\pi/13)$. Thus

$2(c_1s_{1/2}-c_2s_{1/2}+c_3s_{1/2}+c_4s_{1/2}-c_5s_{1/2}-c_6s_{1/2})=\sqrt{13}s_{1/2}$

Next comes the sum-product relation

$2\cos(a)\sin(b)=\sin(a+b)-\sin(a-b)$

from which

$2c_ks_{1/2}=s_{k+1/2}-s_{k-1/2}$

Plugging this into (2) gives a lot of terms, some of which are canceled and others doubled when we combine terms wuth like subscripts. Which terms get doubled determines which diagonals will get into the final sum. For this case $s_{1/2}$ is left unchanged; $s_{3/2},s_{5/2},s_{9/2}$ are doubled and the rest of the terms end up canceled; thus

$-s_{1/2}+2s_{3/2}-2s_{5/2}+2s_{9/2}=\sqrt{13}s_{1/2}$

Now we do two things: first divide by $s_{1/2}$ and identify the resulting ratios with the diagonal/side ratios in the ploygon. To wit,

$s_k/s_{1/2}\equiv D(2k)$

So for $k=1/2$, then $s_k/s_{1/2}= D(1) = 1$. Thus

$-1+2D(3)-2D(5)+2D(9)=\sqrt{13}$

Next adjust the equation algebraically so that the right side matches the target, here by adding $3$ and dividing by $2$:

$1+D(3)-D(5)+D(9)=(3+\sqrt{13})/2=U_{13}$

And there we are. Of course by symmetry $D(p-k)$ will equal $D(k)$, so here we can replace $9$ with $13-9=4$ to get the smallest numbers.

$1+D(3)+D(4)-D(5)=(3+\sqrt{13})/2=U_{13}$

Now it's your turn to fill in the result for $p=53$. Below I give the Legendre symbols for residues $1$ through $26$ from which to form the Gauss sum as rendered in (1):

$(r|53)=+1:\{1,4,6,7,9,10,11,13,15,16,17,24,25\}$

$(r|53)=-1:\{2,3,5,8,12,14,18,19,20,21,22,23,26\}$