I'm following the book "Abel's Theorem in Problems and Solutions" by V.B. Alekseev, where the author introduces schemes of Riemann surfaces in such a way that an arrow indicates passage from one sheet of Riemann surface to another induced by rotation around corresponding branch point.
For example, the function $f_1(z) = \sqrt[3]{z^2-1} + \sqrt{\frac{1}{z}}$ has the following scheme (ex. 314 in book):
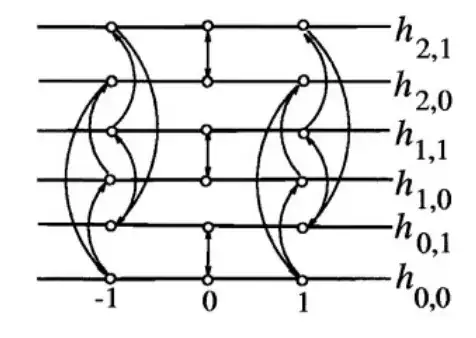
where $h_{0,1} = \sqrt[3]{z^2-1} - \sqrt{\frac{1}{z}},\; h_{1,0} = e^{\frac{2\pi i}{3}}\sqrt[3]{z^2 - 1} + \sqrt{\frac{1}{z}}$ etc. (principal branches).
He then defines monodromy group of such a scheme as a group generated by permutations of sheets of Riemann surfaces, which arise when one interprets arrows on this scheme as permutations of sheets, numbered arbitrarily.
It is then stated (ex. 335 in the book) that such a group is isomorphic to the group generated by permutations of values of multivalued function induced by loops in the input plane around branch points.
For the function $f_1(z)$, the above diagram gives a group $<(12)(34)(56), (135)(246)> \cong \mathbb{Z}_6$. Using a simple Python code, I've observed the following behavior of its values: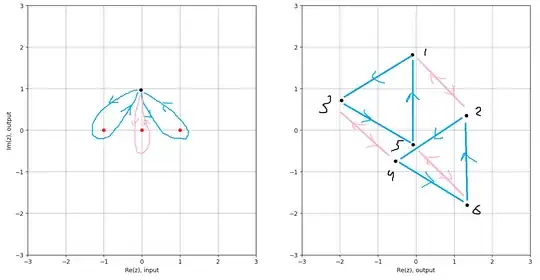 
which agrees with the group from the scheme of this function. Now, when I consider function $f_2(z) = \sqrt[3]{z^2 - 1} + \sqrt{z}$, I observe the following behavior of its values: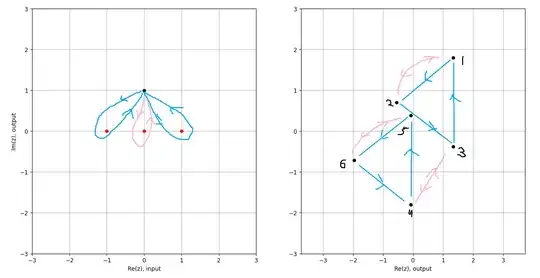 
which seems to suggest the group $<(123)(456), (12)(34)(56)>$, which I believe to be isomorphic to $S_4$. However, from my understanding the scheme of Riemann surface for that function must be the same as for $f_1(z)$, because it has the same branch points and counterclockwise rotation around $z = 0$ still results in minus sign on the square root, while the behavior at $z = \pm 1$ is unchanged. So either I've misinterpreted the statement, or I've made mistake in calculations.
Any help will be appreciated!
