I got some Data to share with OP.
This makes sense only in hyperbolic geometry , where hexagon can/will have less than $6 \times 180 - 360 = 720^\circ$ , while Euclidean geometry will not allow $90 \times 6 = 540^\circ$ around the hexagon.
Using this question which was answered by user aes , I modified the Diagram there to high-light what the question here is talking about :
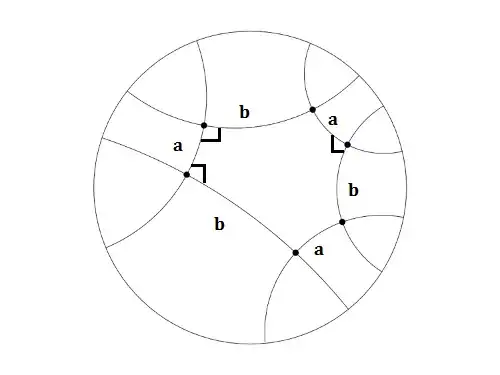
Here , all angles are $90^\circ$ , giving the right-angled hexagon.
We can then see that while we might show the other sides are equal , it is not necessary calculate the $b$ value.
Since OP wanted clarification , which I have given here , I think I should not proceed to the Solution itself.
Still , I will give the very high-level "Proof Out-line" here.
According to standard text books & other sources listed here , every triplet $(a,b,c)$ has a "Single" hexagon with all right-angles with sides $(a,x,b,y,c,z)$ in that order.
Hence , when we have triplet $(a,a,a)$ , that "Single" hexagon must be $(a,x,a,y,a,z)$ , which we can rotate to get $(a,y,a,z,a,x)$ & $(a,z,a,x,a,y)$
We should naturally get back the Original hexagon.
In other words , $x=y=z$
