3

I was hoping someone would help me understand better what a "right-angled hexagon" is in hyperbolic geometry. I know these are glued together somehow to produce hyperbolic pairs-of-pants. The only actual definition I have found in Fenchel's book "Elementary Geometry in Hyperbolic Space" is that of (paraphrase) a cyclically-ordered sextuplet of lines $S_n , n \pmod 6 $ , so that the lines $S_n, S_{n+1}$ are normal to each other (?) , but not the same improper lines and $S_{n-1}, S_{n+1}$ do not coincide...

What do we mean by lines normal to each other, and the rest? Thanks.

RikOsuave
  • 337
  • 1
  • 9

1 Answers1

11

A right-angled hexagon is simply a hexagon in the hyperbolic plane with hyperbolic lines (geodesics) as its edges, and interior angles all right angles:

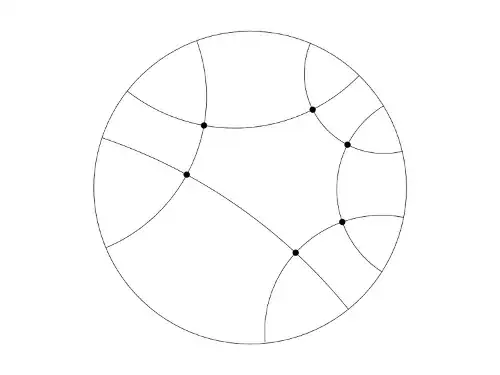
enter image description here

These have lesser total interior angle (and greater total exterior angle) than you'd get in a euclidean hexagon, but that's fine in the hyperbolic plane.

There exists a unique one of these given three non-adjacent side lengths, which is a nice but non-trivial exercise in hyperbolic geometry, and is useful for constructing hyperbolic surfaces from pairs of pants. You can glue two identical ones along three non-adjacent sides to get a pair of pants (and, by the above, you can even specify the cuff lengths for the pair of pants). Then these hyperbolic pairs of pants can be glued to form closed hyperbolic surfaces. If we didn't use right-angled hexagons, the pairs of pants wouldn't have straight boundaries, and the construction wouldn't work.

Here's an image (courtesy David Austin), showing two pairs of pants each built out of two hyperbolic hexagons, which can then be glued to give a hyperbolic genus-2 surface:

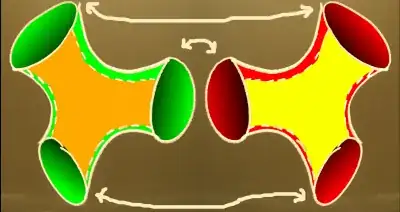
enter image description here

At a more basic level, it can be easily seen that there's one with all side lengths equal, at least: start with a very small hyperbolic hexagon, whose angles will be close to those of Euclidean hexagons (i.e. $2\pi/3$), and then pull the geodesics apart; at some point you will get right angles, because as they get further apart, the angles go to zero.

aes
  • 7,803
  • Ah, I see. Do you know anything about how these are glued to get hyperbolic pairs-of-pants? Is this an obvious thing I am missing? – RikOsuave Dec 21 '14 at 05:14
  • Thanks, nice explanation; one last thing, please, do you know of a nice, clear, non-expert ref. for your reply? – RikOsuave Dec 21 '14 at 05:17
  • I don't have a basic reference in mind. I'll look around briefly. I found this question and some of those references are good, but I'm not sure any are exactly about this stuff and at a basic level. – aes Dec 21 '14 at 05:23
  • Thanks; intermediate level would also work. – RikOsuave Dec 21 '14 at 05:27
  • Ratcliffe, Foundations of Hyperbolic Manifolds is decent. (See the section on hyperbolic trigonometry.) There's also Hubbard, Teichmüller Theory, vol. 1. Neither of these is particularly basic, unfortunately. – aes Dec 21 '14 at 05:31
  • Excellent, thanks for everything. – RikOsuave Dec 21 '14 at 05:32