5

Suppose I have a lower-triangular $d\times d$ matrix $A_d$ where $k$'th row has the following values $$\frac{1}{\sqrt{k}}(\underbrace{1, 1, 1, \ldots, 1}_{k}, 0, 0, 0)$$

What is the smallest singular value of $A_d$ when $d$ is large? Empirically it appears to be approximately:

$$\sigma_\text{min}(A_d)\approx\frac{1}{2\sqrt{d}}$$ Is there a theoretical explanation of this?

Empirical fit for larger values of $d$:

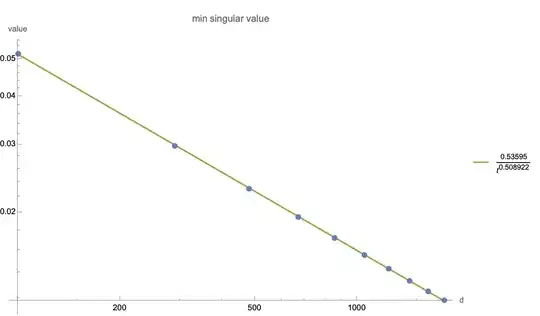
enter image description here

Related observations:

  • largest singular value of $A_d$ grows as $O(\sqrt{d}): $post
  • k'th singular value of $A_d$ appears to decay as $O(1/k)$ (unanswered): post
  • Smallest singular value of some random matrix variables is $O(1/\sqrt{d})$ , Section 5 of Terry Tao's blogpost and Theorem 2.7.8 of his book

Notebook

Yaroslav Bulatov
  • 5,579
  • Have you computed the corresponding right singular vectors? I would guess they are taking advantage of some potential cancellations between the lower rows, so I'd guess that their entries are alternating in sign and concentrated towards the bottom, or something like that. – Qiaochu Yuan Jul 13 '24 at 02:07
  • Are you asking about a specific matrix? The matrix $(1,..,1)^T (1,0,...,0)$ satisfies the stated conditions but the minimum singular value is zero. – copper.hat Jul 13 '24 at 02:16
  • @QiaochuYuan yes, the entries are alternating in sign, and getting larger towards the bottom – Yaroslav Bulatov Jul 13 '24 at 02:20
  • 1
    @copper.hat I can see now that my statement of conditions was imprecise, fixed – Yaroslav Bulatov Jul 13 '24 at 02:26
  • 3
    I don't know if this helps much, but $(A_d^T A_d)^{-1}$ is tridiagonal with a nice form. – arkeet Jul 13 '24 at 03:07

1 Answers1

7

The smallest singular value of $A_d$ is in fact on the order of $\frac1{2\sqrt d}$.

We first compute the inverse: $$A_d^{-1}=\begin{pmatrix}1\\-1&\sqrt2\\&-\sqrt2&\sqrt3\\&&\ddots&\ddots\\&&&-\sqrt{d-1}&\sqrt d\end{pmatrix}.$$ The smallest singular value of $A_d$ is the reciprocal of the largest of $A_d^{-1}$, which is the operator norm. So, we wish to maximize $$v_1^2+\sum_{i=2}^d(v_i\sqrt i-v_{i-1}\sqrt{i-1})^2$$ subject to $v_1^2+\cdots+v_d^2=1$. Define $w_i=(-1)^iv_i\sqrt i$, so that we have $$\sum_{i=1}^d\frac{w_i^2}i=1$$ and wish to maximize $$f(w)=2w_1^2+2w_2^2+\cdots+2w_{d-1}^2+w_d^2+2w_1w_2+\cdots+2w_{d-1}w_d.$$ If the maximum of $f(w)$ is $\sigma^2$, then $\sigma^{-1}$ is the smallest singular value of $A_d$.

On one hand, the fact that $w_1^2+\cdots+w_d^2\leq d$ gives us the bound $$f(w)\leq 2(w_1^2+\cdots+w_d^2)+(w_1^2+w_2^2)+\cdots+(w_{d-1}^2+w_d^2)\leq 4d,$$ so $\sigma^2\leq 4d$ and thus $\sigma^{-1}\geq\frac1{2\sqrt d}$. On the other hand, we can choose a parameter $k$ and let $w_d=\cdots=w_{d-k+1}=\mu$ for $$\mu^2=\frac1{\frac1d+\cdots+\frac1{d-k+1}}.$$ This gives us $$f(w)=\mu^2(4k-3)=\frac{4k-3}{\frac1d+\cdots+\frac1{d-k+1}}\geq\frac{(4k-3)(d-k)}k.$$ Taking $k$ to grow in such a way that $k=\omega(1)$ and $k=o(d)$ gives that $f(w)=4d(1-o(1))$, and so $\sigma^2\geq 4d(1-o(1))$. This means $\sigma^{-1}\leq \frac{1+o(1)}{2\sqrt d}$.

Carl Schildkraut
  • 37,483