7

Suppose I have a triangular $d\times d$ matrix $A$ with constant rows normalized to have Euclidean norm 1. Empirically it appears that operator norm (largest singular value) of such matrix is $\sqrt{d \log 2}$, for large $d$, why?

For instance, for $d=5$ $$A=\left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 & 0 \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ \end{array} \right)$$

with norm $1.94787$.

For larger values of $d$, $\sqrt{d \log 2}$ appears to make a nice fit:

enter image description here

Yaroslav Bulatov
  • 5,579
  • To obtain the order of the matrix norm in terms of $d$, you must provide the definition of the norm you are adopting. It is true that matrix norms are equivalent, i.e., if $M$ and $N$ are two matrix norms on matrices of order $d\times d$, then there exist constants $C_{1}$ and $C_{2}$ such that $C_{1} M(A)\leq N(A) \leq C_{2} M(A)$. But these constants may depend on the dimension $d$. – Medo Apr 16 '24 at 19:48
  • @Medo good point I have clarified to mean operator norm – Yaroslav Bulatov Apr 16 '24 at 20:05
  • It is better to put an explicit definition in the question. – Medo Apr 16 '24 at 20:17
  • 1
    @Medo operator norm of a matrix is fairly standard, no? I've added a link to wikipedia page for operator norm and clarified that for vectors, I'm considering Euclidean norm as "the norm" – Yaroslav Bulatov Apr 16 '24 at 20:36
  • An operator norm for a matrix involves two norms. If the two norms are considered Euclidean norms, then the operator norm becomes equivalent to the largest singular value. This special matrix norm is also called spectral norm, denoted by $| \cdot |_2$. – Amir Apr 19 '24 at 16:37
  • 6
    It actually isn't $\log 2$ but $1/u$ where $u$ is the smallest positive root of $F(u)=\sum_{n=0}^\infty\frac{(-1)^n}{(n!)^2}u^n$ (also known as the zeroth Bessel function after an appropriate change of variable) but I should grant you that your $\log 2$ approximation is correct up to the third digit after the decimal point :lol: – fedja Apr 19 '24 at 22:30

1 Answers1

10

@Fedja already gave the beautiful answer in the comment. Let me try to write out a possible way to obtain it.

Let $M_d$ be your matrix. The first idea is to find the correct "limiting object" of $M_d$. Note that the $(i, j)$-th entry of $N_d = M_dM_d^T$ is given by $\sqrt{\frac{\min(i, j)}{\max(i, j)}}$. Now let's define the ``scaled down" version of $N_d$ as a function $K_d: [0, 1]^2 \to [0,1]$ given by $$K_d(x, y) = \sqrt{\frac{\min(i, j)}{\max(i, j)}}, \forall x \in \left[\frac{i - 1}{d}, \frac{i}{d}\right), y \in \left[\frac{j - 1}{d}, \frac{j}{d}\right).$$ We can regard $K_d$ as a Hilbert-Schmidt operator on $L^2([0,1])$ $$(K_d f)(x) = \int K_d(x, y) f(y)dy.$$ And we can show that, $\newcommand{\norm}[1]{\lVert #1 \rVert}$ $$\norm{M_d}^2 = \norm{N_d} = d\norm{K_d}.$$ Now, $K_d$ converges in $L^2([0,1]^2)$ to the kernel $$K(x, y) = \sqrt{\frac{\min(x, y)}{\max(x, y)}}.$$ So we conclude that $$\lim_{d \to \infty} \frac{\norm{M_d}^2}{d} = \lim_{d \to \infty} \norm{K_d} = \norm{K}.$$ The rest of the problem is to compute $\norm{K}$. I'll be a bit sloppy here, and some details are omitted. The norm of $K$ is equivalent to solving the following optimization problem $$\norm{K} = \max \int_{[0, 1]^2} \sqrt{\frac{\min(x, y)}{\max(x, y)}} f(x) f(y) dxdy, \text{given} \int_{0}^1 f(x)^2 dx = 1.$$ Letting $g(x) = f(x) / \sqrt{x}$, the problem becomes $$\norm{K} = \max \int_{[0, 1]^2} \min(x, y) g(x) g(y) dxdy, \text{given} \int_{0}^1 x g(x)^2 dx = 1.$$ Note that $$\int_{[0, 1]^2} \min(x, y) g(x) g(y) dxdy = \int_0^1 \left(\int_x^1 g(t) dt\right)^2 dx.$$ So, setting $\phi(x) = \int_x^1 g(t) dt$, we have $$\norm{K} = \max \int_0^1 \phi(x)^2 dx, \text{given} \int_{0}^1 x \phi'(x)^2 dx = 1, \phi(1) = 0.$$ In other words $$\norm{K}^{-1} = \min \int_0^1 x \phi'(x)^2 dx, \text{given} \int_{0}^1 \phi(x)^2 dx = 1, \phi(1) = 0.$$ This can be solved via Calculus of variations. Specifically, the optimal $\phi$ should satisfy $$(x \phi'(x))' = -\lambda \phi(x), \phi(1) = 0$$ and $\norm{K}^{-1}$ is equal to the smallest $\lambda$ such that this can hold.

Now we can solve this via Taylor expansion, to obtain up to a scalar $$\phi(x) = \sum_{n = 0}^\infty \frac{(-\lambda x)^n}{(n!)^2}.$$ So in conclusion, $\norm{K}^{-1}$ is the smallest solution $\lambda$ to $$\phi(1) = \sum_{n = 0}^\infty \frac{-\lambda^n}{(n!)^2} = 0$$ which is @Fedja's answer.

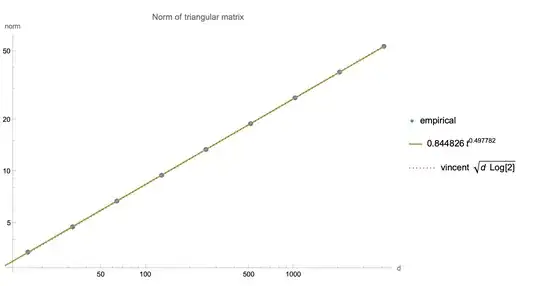
Numerics: $\lambda \approx 1.446$, $(\log 2)^{-1} \approx 1.443$.

abacaba
  • 11,210