Surjective homomorphism $\mathbb Z * \mathbb Z \to C_2 * C_3$; can my proof be rescued?

Question

I'm trying to solve the following problem from Aluffi's Algebra: Chapter 0:

Show that there is a surjective homomorphism $\mathbb Z * \mathbb Z \to C_2 * C_3$.

This problem has been discussed on the site before, but not (I think) from the particular angle that I will put forward here.

At this point in the text we do not have any explicit constructions of $\mathbb Z * \mathbb Z$ and $C_2 * C_3$; we know only that they are coproducts in $\mathsf{Grp}$. Hence I have been trying to solve the problem by using universal properties.

As seen below, I have been able to prove this: there exists an epimorphism $\mathbb Z * \mathbb Z \to C_2 * C_3$. I have gleaned from the internet that epimorphisms in $\mathsf{Grp}$ are also surjective, but the proof of that fact is far beyond my current knowledge (and beyond what has been covered in the text).

Is there some other (hopefully more elementary) way to rescue my (attempted) proof?

My attempt

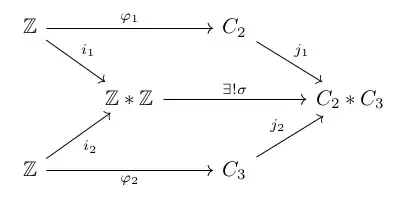
Consider the following diagram:

Here $i_1, i_2, j_1, j_2$ are the canonical homomorphisms associated with the two coproducts, and $\varphi_1, \varphi_2$ are surjective homomorphisms (there are obvious ones to choose from). By the universal property of the coproduct there is a unique homomorphism $\sigma$ making the diagram commute.

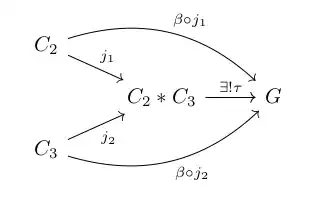
Next, let us show that $\sigma$ is an epimorphism. Hence let $G$ be an arbitrary group and $\beta, \beta': C_2 * C_3 \to G$ be arbitrary homomorphisms satisfying $\beta \circ \sigma = \beta' \circ \sigma$. Then

$$\beta \circ j_1 \circ \varphi_1 = \beta \circ \sigma \circ i_1 = \beta' \circ \sigma \circ i_1 = \beta' \circ j_1 \circ \varphi_1,$$

which implies that $\beta \circ j_1 = \beta' \circ j_1$, since $\varphi_1$ is (clearly) an epimorphism. Similarly $\beta \circ j_2 = \beta' \circ j_2$. Again by universal property, there is a unique homomorphism $\tau$ making the following diagram commute:

But setting $\tau = \beta$ or $\tau = \beta'$ both make the diagram commute; hence $\beta = \beta'$. This shows that $\sigma$ is an epimorphism.

Not yet proven: $\sigma$ is surjective.

Remark

I notice now that there is a very similar solution suggested here. However, it has the same problem as mine; it only shows that there is an epimorphism.

Answer 1

The key is that the coproduct is generated by the canonical images of the groups it is a coproduct of.

Lemma. Let $G_1$ and $G_2$ be groups, and let $\iota_j\colon G_j\to G_1*G_2$ be the canonical embeddings into the coproduct. Then $G_1*G_2=\langle \iota_1(G_1),\iota_2(G_2)\rangle$.

Proof. Let $K=\langle\iota_1(G_1),\iota_2(G_2)\rangle$, which is a subgroup of $G_1*G_2$. Let $j_1\colon G_1\to K$ and $j_2\colon G_2\to K$ be the co-restrictions of $\iota_1$ and $\iota_2$ to $K$ (that is, they are the same underlying maps, but we put $K$ to be the codomain rather than $G_1*G_2$).

By the universal property of the coproduct, there exists a unique group homomorphism $g\colon G_1*G_2\to K$ such that $g\circ\iota_1 = j_1$ and $g\circ\iota_2=j_2$. Note that $g$ is surjective, since the image of $g$ contains the images of $j_1$ and $j_2$, which together generate $K$.

On the other hand, if we let $h\colon K\hookrightarrow G_1*G_2$ be the canonical embedding, we have $\iota_1 = h\circ j_1$ and $\iota_2 = h\circ j_2$.

Now we have the maps $h\colon K\to G_1*G_2$ and $g\colon G_1*G_2\to K$. We know that $h$ is one-to-one and $g$ is surjective. We want to show that $h$ is also surjective. That suffices, since $h$ is the canonical inclusion of the subgroup $K$ into $G_1*G_2$.

To that end, we show that $h\circ g\colon G_1*G_2\to G_1*G_2$ is the identity map. Indeed, we have maps $(h\circ g)\circ\iota_1\colon G_1\to G_1*G_2$ and $(h\circ g)\circ\iota_2\colon G_2\to G_1*G_2$. By construction, $$\begin{align*} (h\circ g)\circ \iota_1 &= h\circ(g\circ \iota_1)=h\circ j_1 = \iota_1,\\ (h\circ g)\circ \iota_2 &= h\circ(g\circ \iota_2)=h\circ j_2 = \iota_2. \end{align*}$$ Now we use the uniqueness of the universal property: we know that there exists a unique $\Psi\colon G_1*G_2\to G_1*G_2$ such that $\Psi\circ\iota_i = (h\circ g)\circ \iota_i$. One such map is of course $h\circ g$. But we just saw that another such map is $\mathrm{id}_{G_1*G_2}$. Therefore, we must have $h\circ g = \mathrm{id}_{G_1*G_2}$. This proves that $h$ has a right inverse and $g$ a left inverse, and therefore that $h$ is surjective and $g$ is injective. Thus, the canonical embedding $h\colon\langle \iota_1(G_1),\iota_2(G_2)\rangle \hookrightarrow G_1*G_2$ is surjective. Therefore, $$G_1*G_2 = \langle \iota_1(G_1),\iota_2(G_2)\rangle,$$ as claimed. $\Box$

---

Remark. This holds for an arbitrary coproduct (any number of co-factors, not just two). Also, the argument is only using the universal properties and the notion of "substructure generated", so the argument holds in any category of $\Omega$-algebras that has a coproducts.

---

Now, you have your $\sigma\colon\mathbb{Z}*\mathbb{Z}\to C_2*C_3$. This $\sigma$ satisfies that $$\begin{align*} \sigma\circ\iota_1 &= j_1\circ\phi_1\\ \sigma\circ\iota_2 &= j_2\circ\phi_2. \end{align*}$$ We also know that both $\phi_1$ and $\phi_2$ are surjective. Thus, the image of $\sigma$ contains the image of $j_1$, and contains the image of $j_2$. Thus, $$C_2*C_3 = \langle j_1(C_2),j_2(C_3)\rangle \subseteq \sigma(\mathbb{Z}*\mathbb{Z})\subseteq C_2*C_3,$$ which proves that $\sigma$ is surjective, as desired.