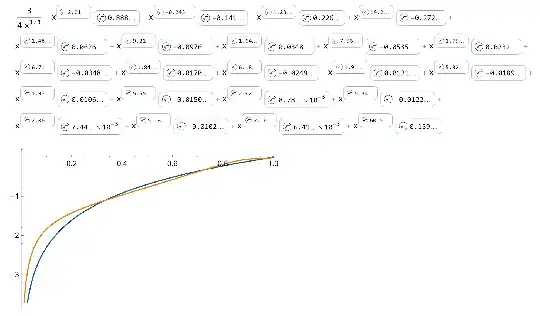
Let's approximate $\log x$ on the interval $(0,1)$ by a power function $a x^b$ to minimize the integral of the squared difference $$\delta_0(a,b)=\int_0^1\left(\log x-a x^b\right)^2dx.\tag1$$ It's easy to verify that the minimum is attained at $a_0=-\frac34,\,b_0=-\frac13$ that gives the approximation $$\log x=-\tfrac34x^{-1/3}+\mathcal R(x),\tag2$$ where $\mathcal R(x)$ is the error term. Now, let's again approximate $\mathcal R(x)$ by a power function $a x^b$ to minimize $$\delta_1(a,b)=\int_0^1\left(\mathcal R(x)-a x^b\right)^2dx=\int_0^1\left(\log x-\left(-\tfrac34x^{-1/3}+a x^b\right)\right)^2dx.\tag3$$ The minimum is attained at $$\begin{align}a_1&=\frac{17}4-\sqrt{58} \sin \left[\frac13 \arctan \left(\frac{433}{33\sqrt7}\right)\right]\approx0.88760008404...,\\b_1&=\frac{1}{3}+\frac{4}{3} \sqrt{2} \cos \left[\frac{1}{3} \arctan\left(\frac{\sqrt{7}}{11}\right)\right]\approx2.21311796239...,\end{align}\tag4$$ which are algebraic numbers of degree $3^\dagger$. If we repeat this process once again, we will get the next term $a_2x^{b_2}$, where $$a_2\approx-0.1406322691...,\, b_2\approx-0.2430593194...\tag5$$ are algebraic numbers of degree $15^\ddagger$, for which I don't know any closed form. The following steps will similarly produce pairs of algebraic numbers of higher degrees, resulting in an approximation of $\log x$ on the interval $(0,1)$ by a generalized power series $$\log x\approx-\tfrac34x^{-1/3}+a_1x^{b_1}+a_2x^{b_2}+\dots,\tag6$$ where each next term causes the integral of the squared error term to progressively decrease. The powers $b_n$ and coefficients $a_n$ are not monotone and do not exhibit any clear pattern (although the coefficients generally tend to decrease in absolute value, with some sporadic spikes).
Question: What does the series $(6)$ converge to? Does it converge to $\log x$ on any interval?
If it does converge to $\log x$, then empirically the convergence appears to be quite slow and erratic.
${^\dagger}$ The corresponding minimal polynomials are $\small64 z^3-816 z^2+684 z-9$ and $\small9 z^3-9 z^2-21 z-7.$
${^\ddagger}$ The corresponding minimal polynomials are $\small5035261952 z^{15}+180729937920 z^{14}+19190513664 z^{13}-60948402536448
z^{12}-383744783499264 z^{11}+6281308897579008 z^{10}+50474690060451840
z^9-155303784466089984 z^8-1906255797863421024 z^7+805421030545306296
z^6+670389754270702752 z^5+127003127714790264 z^4+8514399973766202
z^3+130643635592430 z^2-127629387774 z-79827687$
and
$\small118098 z^{15}-1299078 z^{14}-15628302 z^{13}-52936335 z^{12}-55068660
z^{11}+119832291 z^{10}+512627130 z^9+898647291 z^8+984822786 z^7+742152591
z^6+396538632 z^5+150470676 z^4+39697272 z^3+6920496 z^2+715716 z+33172.$
Although the polynomials look scary, they are quite nice in some sense, e.g. $\small5035261952=2^{21}\cdot7^4$ and $\small79827687=3^8\cdot23^3,$ and they also can be factored into quintics over some $\mathbb Q[q]$ with $q$ expressible in radicals.