What is the number of lattice paths of length 16 from the point (0,0) to (8,8) that go through (4,4) but don't go through (1,1), (2,2), (3,3)

Question

what is the number of lattice paths of length 16 from $(0,0)$ to $(8,8)$ that go through $(4,4)$, don't go through $(1,1), (2,2), (3,3)$, and don't go over $y=x$?

Here's what I tried:

since we can't go through those 3 points above, we can first go to $(3,2)$ from $(1,0)$ (there is one forced move from $(0,0)$ to $(1,0))$ without going over the line $y=x-1$. Without the condition of not going over the line, the number is ${(3-1)+(2-0) \choose 2}={4 \choose 2}=6$. with the condition, we can try the reflection method to find the "bad cases". so it is an injective match with the paths from $(1,0)$ to (2,3) that touch the line $y=x$ and that is 1 move to the right and 3 moves up, so the number of ways to choose is ${1+3 \choose 1}={4 \choose 1}=4$ and then 6-4=2, and then we do a similar thing for the path from $(3,2)$ to $(4,4)$ and $(8,8)$ but I am not sure of my answer and method.

Answer 1

The number of paths of length $2n$ from $(0, 0)$ to $(n, n)$ that do not go over $y = x$ is known to be the $n$th Catalan number $$ C_n = \frac{1}{n+1}\binom{2n}{n} = \binom{2n}{n} - \binom{2n}{n-1}. $$ There's an obvious shift bijection that generalizes this to count paths of length $2n$ from $(a, b)$ to $(a + n, b + n)$ that do not go above $y = x - a + b$: just send $(x, y) \mapsto (x + a, y + b)$.

In your problem, we have to take the first step from $(0, 0)$ over to $(1, 0)$ and also the eighth step from $(4, 3)$ up to $(4, 4)$, so when counting paths we just need to enumerate those of length $8 - 2 = 6$ from $(1, 0)$ to $(4, 3)$ that don't go above $y = x - 1$. This is an example of the shifted Catalan problem with $(a, b) = (1, 0)$ and $n = 3$, so there are $C_3 = 5$ such.

Analogously, we also have to count paths of length $8$ from $(4, 4)$ to $(8, 8)$, another shifted Catalan counting problem, this time with

$$ n = 4 \quad\text{and}\quad (a, b) = (4, 4), \quad\text{so}\quad C_4 = 14. $$

Every path involves an independent choice of one of the first type and one of the second type of paths, so the total count is

$$ C_3 \cdot C_4 = 5 \cdot 14 = 70. $$

Answer 2

Ordinarily, if the constraints were merely against crossing $~(1,1), ~(2,2),~$ and $~(3,3),~$ then I would say that the indirect approach of Inclusion-Exclusion is best. See this article for an introduction to Inclusion-Exclusion. Then, see this answer for an explanation of and justification for the Inclusion-Exclusion formula.

However, the added constraint that you are always on or to the right of the line $~x = y~$ makes it more difficult to use Inclusion-Exclusion. Therefore, I agree with the original poster's decision to use some direct approach, even though such an approach does not generalize well, and even though such an approach tends to facilitate analytical error. You simply have to be very careful how things are handled.

---

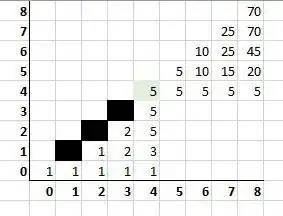
At this point, hoping to gain insight into the harder part of the problem, I would first ask myself what are all of the ways of going satisfactorily from $~(4,4)~$ to $~(8,8).$ So, you must combine $~4~$ vertical moves with $~4~$ horizontal moves, such that at no point, do the number of vertical moves already taken outnumber the number of horizontal moves already taken.

Letting $~(x,y)~$ denote that from $~(4,4)~$ you have taken $~x~$ horizontal moves and $~y~$ vertical moves, on your way towards $~(8,8),~$ any path chosen must never have $~x < y.~$

The challenge here is to strive for some (moderate) form of elegance, and still break the cases into mutually exclusive possibilities.

The total number of ways of going from $~(4,4)~$ to $~(8,8)~$ without any regard for whether the $~x = y~$ line is crossed must be $~\displaystyle \binom{8}{4} = 70.$

So, from this number, I will deduct the number of ways that the $~x = y~$ line is first crossed at either $~(4,4), ~(5,5), ~(6,6),~$ or $~(7,7).$ I will let the counters $~N_1, \cdots, N_4~$ represent each of these respective enumerations.

• The $~x = y~$ line is first crossed at $~(4,4).~$
  This means that the first move is vertical, rather than horizontal.
  Invoking considerations of symmetry, you must have that
  $~\displaystyle N_1 = \frac{70}{2} = 35.$

• The $~x = y~$ line is first crossed at $~(5,5).~$
  So, the first move was horizontal, and the second move was vertical.
  Then, there were $~3~$ vertical and $~3~$ horizontal moves pending.
  Again, invoking considerations of symmetry, you must have that
  $~\displaystyle N_2 = \displaystyle \frac{\binom{6}{3}}{2} = 10.$

• The $~x = y~$ line is first crossed at $~(6,6).~$
  Letting (for example) HHVV denote that there were two horizontal moves taken, and then two vertical moves taken, the possibilities are
  HHVV and HVHV.
  Then, invoking considerations of symmetry similar to the last section, the number of ways of violating the $~x = y~$ line is then
  $~\displaystyle \displaystyle \frac{\binom{4}{2}}{2} = 3.$
  Therefore, $~N_3 = 2 \times 3 = 6.$

• The $~x = y~$ line is first crossed at $~(7,7).~$
  Here, the possibilities of satisfactorily reaching $~(7,7)~$ are
  HHHVVV, HHVHVV, HHVVHV, HVHHVV, HVHVHV : $~5~$ ways.
  Then, there is one pending V move, and one pending H move, and the V move must be first. Therefore, $~N_4 = 5.$

Therefore, the number of satisfactory ways of going from $~(4,4)~$ to $~(8,8)~$ is

$$70 - (N_1 + N_2 + N_3 + N_4) = 70 - (35 + 10 + 6 + 5) = 14. \tag1 $$

Just to be clear, if there was no constraints on whether $~(1,1), ~(2,2),~$ or $~(3,3)~$ were crossed, then the overall enumeration would be

$$14^2.$$

However, the added constraints must be accommodated.

So, I regard the first half of the problem as complete, and I will then strive to use the insights from this half of the problem in the 2nd half of the problem

---

So, in the first half of the problem, there were $~14~$ ways of going from $~(4,4)~$ to $~(8,8),~$ staying on or to the right of the $~x = y~$ line. When going from $~(0,0),~$ to $~(4,4),~$ staying on or to the right of the $~x = y~$ line, how many ways are there of having the first violation be landing on either $~(1,1), ~(2,2),~$ or $~(3,3) ~?$

I will let $~M_1, ~M_2,~$ and $~M_3~$ denote the number of ways that the path from $~(0,0),~$ to $~(4,4)~$ is always on or to the right of the $~x = y~$ line, and where the first violation is at $~(1,1), ~(2,2),~$ or $~(3,3), ~$ respectively.

The analysis of the previous section may be piggy-backed into this section, as long as it is done very carefully.

• To compute $~M_1,~$ notice that the first two moves must be HV. Now, the possibilities of completing the journey to $~(4,4),~$ always staying on or to the right of the $~x = y~$ line are
  HHHVVV, HHVHVV, HHVVHV, HVHHVV, HVHVHV.
  Notice that the line above matches the first part of the computation of $~N_4~$ from the previous section.
  So, you have that $~M_1 = 5.~$

• To compute $~M_2,~$ notice that the first four moves must be HHVV. Now, the possibilities of completing the journey to $~(4,4),~$ always staying on or to the right of the $~x = y~$ line are
  HHVV, HVHV.
  Notice that the line above matches the first part of the computation of $~N_3~$ from the previous section.
  So, you have that $~M_2 = 2.~$

• To compute $~M_3,~$ notice that the first 6 moves must be either
  HHHVVV or HHVHVV.
  Then, the last two moves must be HV.
  So, $~M_3 = 2.$

Therefore, the computation for this portion of the answer is

$$14 - (M_1 + M_2 + M_3) = 14 - (5 + 2 + 2) = 5. \tag2 $$

---

Combining (1) above and (2) above, the overall enumeration is

$$14 \times 5.$$

Answer 3

It's fairly easy to find the number of valid paths from $(0,0)$ by filling in the number of paths in an array starting at $(0,0)$ (one path) and working to the right and up, adding one row of numbers at a time and keeping in mind the constraints on valid paths. The result:

For example, having found that the number of paths to $(4,0)$ is $1$ and the number of paths to $(3,1)$ is $2$, we know that the number of paths to $(4,1)$ is $1+2=3$.