Product of lengths in a disk of area $\frac{\pi}{e}$

Question

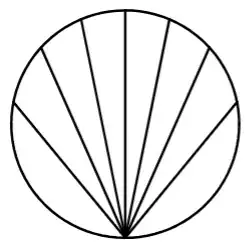
A disk of area $\dfrac{\pi}{a}$ is divided into $n$ regions of equal area by line segments from a point on the edge.

Here is an example with $n=8$.

Let $P(a,n)=\text{product of lengths of the line segments}$.

What is $\lim\limits_{n\to\infty}P(e,n)$ ? ($e$ is Euler's constant)

Why I chose $a=e$

Here are plots of $P(a,n)$ against $n$ with $a=0.99e$, $\space a=e$ and $\space a=1.01e$.

It seems that if $a<e$ then $\lim\limits_{n\to\infty}P(a,n)=\infty$, and if $a>e$ then $\lim\limits_{n\to\infty}P(a,n)=0$.

So $a=e$ seems to be a critical value.

Here are the $P(e,n)$ values that I got; some of these appear in the graph above.

$P(e,2)\approx1.2131$
$P(e,3)\approx1.3682$
$P(e,4)\approx1.4937$
$P(e,5)\approx1.6007$
$P(e,6)\approx1.6946$
$P(e,7)\approx1.7790$
$P(e,12)\approx2.1120$
$P(e,24)\approx2.6452$
$P(e,48)\approx3.3194$
$P(e,96)\approx4.1717$
$P(e,192)\approx 5.2476$

(I calculated these values "manually": that is, I used desmos to get an approximate solution to $x−\sin x=\frac{2k\pi}{n}$ with individual $k$ values, then I used those $x$ values and Excel to approximate $P(e,n)$.)

What makes this difficult

What makes my question difficult for me, is that I cannot find exact expressions for the lengths. For example, with $a=e$ and $n=8$, the length of the shortest line segments is $\frac{2}{\sqrt{e}}\sin \left(\frac{x}{2}\right)$ where $x-\sin x=\frac{\pi}{4}$.

I am aware of Kepler's equation, but that doesn't seem to help.

Context

This question was inspired by the following remarkable fact: If $n$ evenly spaced points are drawn on a unit circle, and line segments are drawn from one point to each of the other points, then the product of lengths of the line segments equals $n$ (proof).

Related question: Conjectured connection between $e$ and $\pi$ in a semidisk

Update

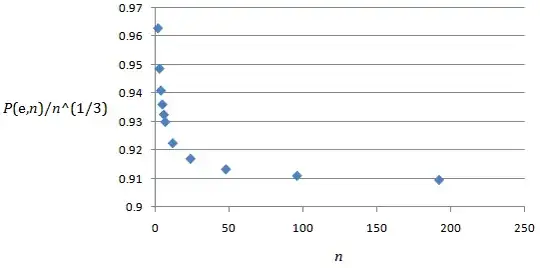
@Carl Schildkraut's answer shows that $\lim\limits_{n\to\infty}\frac{P(e,n)}{n^{1/3}}=\frac{e^{1/2}}{6^{1/3}}\approx0.9073$.

Here is a plot of $\frac{P(e,n)}{n^{1/3}}$ against $n$.

Answer 1

Comment that's too long for a comment:

The proportion of the circle's area cut off by an arc with angle $\theta$ is $A(\theta) = \frac1{2\pi}(\theta-\sin\theta)$, and the length of the corresponding segment is $\frac2{\sqrt a}\sin\frac\theta2$. The geometric mean of the lengths of the segments should then be approximated by exponentiating the integral of the logarithm of the length function when the endpoint is parametrized by $A^{-1}(y)$, namely $$ \exp\biggl( \int_0^1 \log\Bigl( \frac2{\sqrt a} \sin\frac{A^{-1}(y)}2 \Bigr)\,dy \biggr) = \exp\biggl( \int_0^{2\pi} \log\Bigl( \frac2{\sqrt a} \sin\frac\theta2 \Bigr) \frac1{2\pi}(1-\cos\theta)\,d\theta \biggr). $$ It turns out that this integral equals $0$ precisely when $a=e$, which explains the critical point phenomenon. Since we're asking about the product itself and not the geometric mean, we would need to look at the rate of convergence of the Riemann sums of this integral to the integral itself.

Answer 2

Here's a sketch of an argument, following the paradigm given in Greg Martin's answer to compute the behavior of $P(e,n)$. Our conclusion is that $$\lim_{n\to\infty}\frac{P(e,n)}{n^{1/3}}=\frac{e^{1/2}}{6^{1/3}}\approx 0.9073.$$

---

Let $A(\theta)=\frac1{2\pi}(\theta-\sin\theta)$, so that $$\log P(e,n)=\sum_{k=1}^{n-1}\log\left(\frac 2{\sqrt e}\sin\frac{A^{-1}(k/n)}2\right).$$ We leave as an exercise the fact that $$\int_0^1\log\left(\frac 2{\sqrt e}\sin\frac{A^{-1}(y)}2\right)dy=0,$$ so that, if $\delta=1/(2n)$, $$\log P(e,n)=\sum_{k=1}^{n-1}\left[\log\left(\sin\frac{A^{-1}(k/n)}2\right)-\frac1{2\delta}\int_{k/n-\delta}^{k/n+\delta}\log\left(\sin\frac{A^{-1}(y)}2\right)dy\right]-E_0,$$ with $$E_0=\frac1\delta\int_0^\delta\log\left(\frac 2{\sqrt e}\sin\frac{A^{-1}(y)}2\right)dy.$$ Note that the summands do not change if $k$ is replaced by $n-k$. As in Part 2 of my previous answer to a similar question, one can show that the terms with $k$ far from $0$ or $n$ are small, so that $$\log P(e,n)=-E_0+o(1)+2\sum_{k=1}^\infty\lim_{n\to\infty}\left[\log\left(\sin\frac{A^{-1}(k/n)}2\right)-\frac1{2\delta}\int_{k/n-\delta}^{k/n+\delta}\log\left(\sin\frac{A^{-1}(y)}2\right)dy\right].$$ We now evaluate the behavior of these terms. Since $A(\theta)\approx \frac{\theta^3}{12\pi}$ near $\theta=0$, we have $$\sin\frac{A^{-1}(y)}2=\frac{(12\pi y)^{1/3}}2(1+o(1))=\left(\frac{3\pi y}2\right)^{1/3}(1+o(1));$$ since, for each fixed $k$ (or for $E_0$), the $y$-values we consider are tending to $0$ like some constant times $1/n$, this $o(1)$ term can be shown to be $O(n^{-2/3})$. Letting $c=(3\pi/2)^{1/3}$, $x=k/n$ and trusting that the errors turn out to be small, we have \begin{align*} E_k&:=\log\left(\sin\frac{A^{-1}(k/n)}2\right)-\frac1{2\delta}\int_{k/n-\delta}^{k/n+\delta}\log\left(\sin\frac{A^{-1}(y)}2\right)dy\\ &\approx \log(cx^{1/3})-\frac1{2\delta}\int_{k/n-\delta}^{k/n+\delta}\log(cy^{1/3})dy\\ &=\frac13\left(\log x-\frac1{2\delta}\int_{x-\delta}^{x+\delta}\log y dy\right)\\ &=\frac1{6\delta}\left[(x-\delta)\left(\log\left(1-\frac\delta x\right)-1\right)-(x+\delta)\left(\log\left(1+\frac\delta x\right)-1\right)\right]\\ &=\frac{2k+1}6\left(1-\log\left(1+\frac1{2k}\right)\right)+\frac{2k-1}6\left(\log\left(1-\frac1{2k}\right)-1\right). \end{align*} Applying a similar argument to $E_0$ gives that \begin{align*} E_0 &=\frac{\log 2-1}3+\log\left(\frac 2{\sqrt e}\right)+\log\left(\sin\frac{A^{-1}(\delta/2)}2\right)+o(1)\\ &=\frac13\log\left(\frac{6\pi}{e^{5/2}n}\right)+o(1). \end{align*} So, $$\log P(e,n)=o(1)+\frac13\log\left(\frac{e^{5/2}n}{6\pi}\right)+2\sum_{k=1}^\infty \frac{2k+1}6\left(1-\log\left(1+\frac1{2k}\right)\right)+\frac{2k-1}6\left(\log\left(1-\frac1{2k}\right)-1\right).$$ This sum can be found to be $\frac{\log\pi-1}6$, so that $$\log P(e,n)=\frac13\log\left(\frac{e^{3/2}n}{6}\right)+o(1).$$ This implies $$P(e,n)=\left(\frac{e^{3/2}n}{6}\right)^{1/3}(1+o(1)),$$ which gives the result.