4

Let $F$ be the splitting field of an irreducible quartic polynomial $f \in \Bbb Q[x]$.

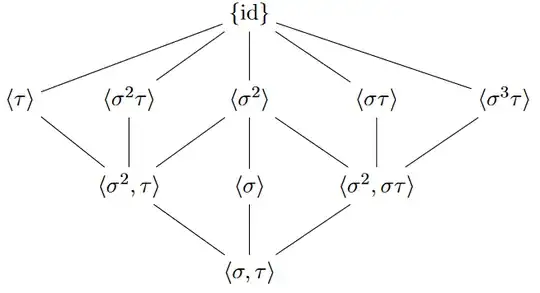
If Galois group of $F/\Bbb Q$ is $D_4$, I try to determine all intermediate subfields explicitly.

$D_4=⟨σ,τ⟩$, $σ=(1234)$, $τ=(24)$, written as permutations of roots $α_1,α_2,α_3,α_4$ of $f$.

(the product $σ τ$ represents the permutation $τ(σ(·))$)

enter image description here

All subgroup relations shown above are subgroups of index $2$, so they correspond to field extensions of degree $2$.

Let $∆$ be the discriminant of $f$.

Then I found

\begin{array}{l} F^{\{\text{id}\}}=ℚ[α_1,α_2,α_3,α_4]\\ F^{⟨τ⟩}=ℚ[α_1]=ℚ[α_3]=F^{⟨σ^2,τ⟩}[α_1-α_3]\\ F^{⟨σ^2τ⟩}=ℚ[α_2]=ℚ[α_4]=F^{⟨σ^2,τ⟩}[α_2-α_4]\\ F^{⟨σ^2⟩}=F^{⟨σ⟩}[α_1-α_2+α_3-α_4]=F^{⟨σ^2,στ⟩}[α_1-α_2+α_3-α_4]=F^{⟨σ^2,τ⟩}[(α_1-α_3)(α_2-α_4)]\\ F^{⟨στ⟩}=ℚ[α_1-α_2-α_3+α_4]=F^{⟨σ^2,στ⟩}[α_1-α_2-α_3+α_4]\\ F^{⟨σ^3τ⟩}=ℚ[α_1+α_2-α_3-α_4]=F^{⟨σ^2,στ⟩}[α_1+α_2-α_3-α_4]\\ F^{⟨σ^2,τ⟩}=ℚ[α_1+α_3]=ℚ[α_2+α_4]=ℚ[α_1-α_2+α_3-α_4]=ℚ[α_1α_3]=ℚ[α_2α_4]\\ F^{⟨σ⟩}=ℚ[(α_1-α_3)(α_2-α_4)(α_1-α_2+α_3-α_4)]\\ F^{⟨σ^2,στ⟩}=ℚ[(α_1-α_3)(α_2-α_4)]=ℚ[\sqrt{\Delta}]\\ F^{⟨σ,τ⟩}=ℚ \end{array} Is this correct?

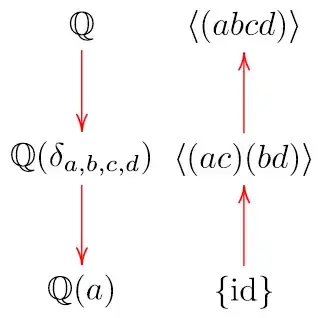
When the Galois group of $f$ is $C_4$, the list of intermediate subfields is enter image description here

where $\delta_{a,b,c,d}=(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$.

When the Galois group of $f$ is $V_4$,

$a+b,ab$ are fixed by $⟨(12)(34)⟩$. By irreducibility of $f$, $(x-a)(x-b)\notinℚ[x]$, so $a+b,ab$ are not both in $ℚ$. Therefore $F^{⟨(12)(34)⟩}=ℚ[a+b,ab]$.

Similarly, $F^{⟨(13)(24)⟩}=ℚ[a+c,ac]$, $F^{⟨(14)(23)⟩}=ℚ[a+d,ad]$.

so the list of intermediate subfields is

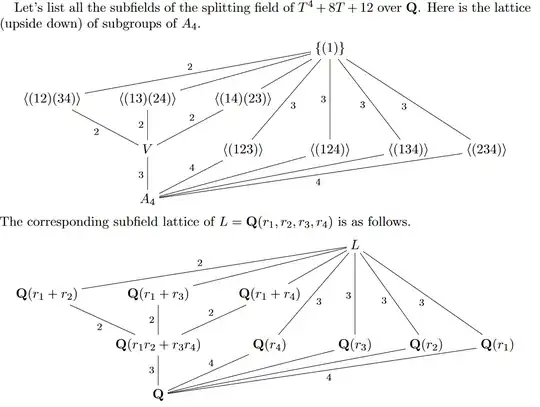
enter image description here

I found on page 8 the list of all intermediate subfields when the Galois group of $f$ is $A_4$

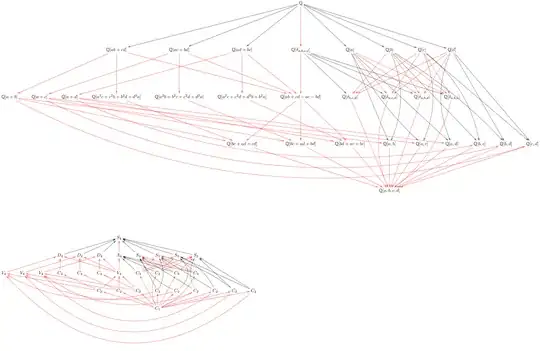
enter image description here

Similarly, I made a list of all intermediate subfields when the Galois group of $f$ is $S_4$. Is it correct? Thanks.

I posted the question about $\langle(1234)\rangle$ here:Is $\Bbb Q[a^2b+b^2c+c^2d+d^2a]$ the fixed field of the subgroup $\langle(1234)\rangle$ of Galois group $S_4$?

enter image description here

In the above diagram, red arrows are normal extensions/subgroups, black arrows are non-normal extensions/subgroups, $a,b,c,d$ are roots of $f$, and $\delta_{a,b,c}=(a-b)(a-c)(b-c),\delta_{a,b,c,d}=(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$.

hbghlyj
  • 5,361
  • I'm a little confused with your notation. Typically $\mathbb Q[\alpha, \dots]$ denotes a polyomial ring over $\mathbb Q$ in indeterminates $\alpha, \dots$ Round parentheses are usually used to indicate fields with adjoined elements, e.g. $\mathbb Q(\alpha, \beta, \dots)$. – Randy Marsh May 03 '24 at 07:02
  • 4
    @RandyMarsh I thought they are the same for algebraic extensions, like: $\Bbb Q[\sqrt2]=\Bbb Q(\sqrt2)$. – hbghlyj May 03 '24 at 07:50
  • 1
    @RandyMarsh For algebraic field extensions, we have $k[\alpha]=k(\alpha)$. Consider $k(\alpha,\beta)=(k(\alpha))(\beta)$ and $k[\alpha,\beta]=(k[\alpha])[\beta]$. – Drinzjeng Triang May 05 '24 at 03:15

0 Answers0