Given a parabola, does the orthocenter of a triangle of tangents lie on the directrix?

Question

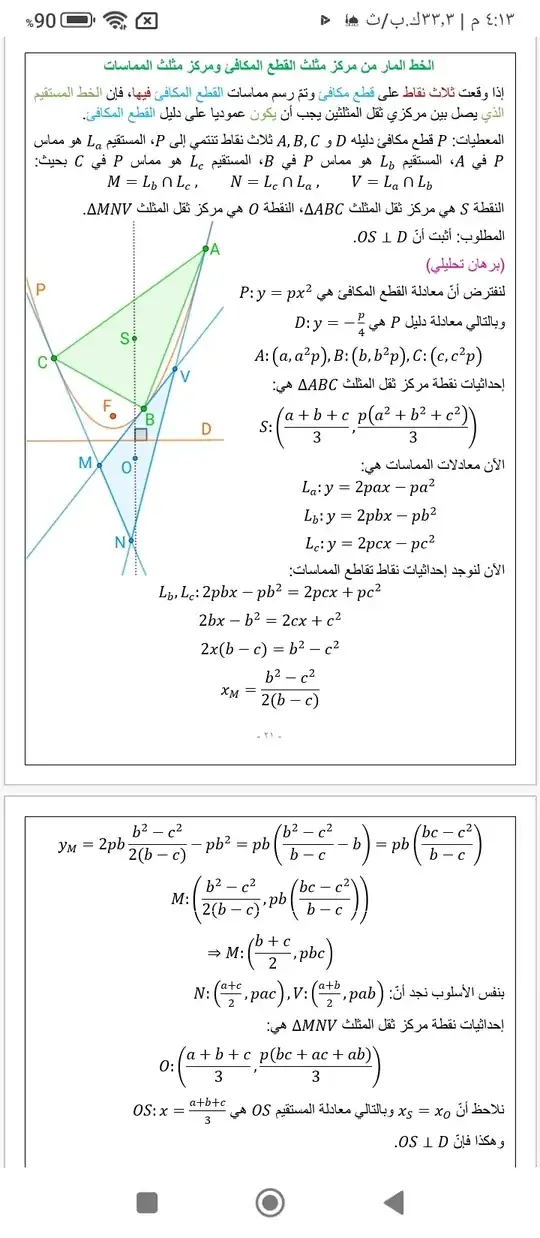
I just came up with a nice parabola property, I don't know if it's already discovered or not. 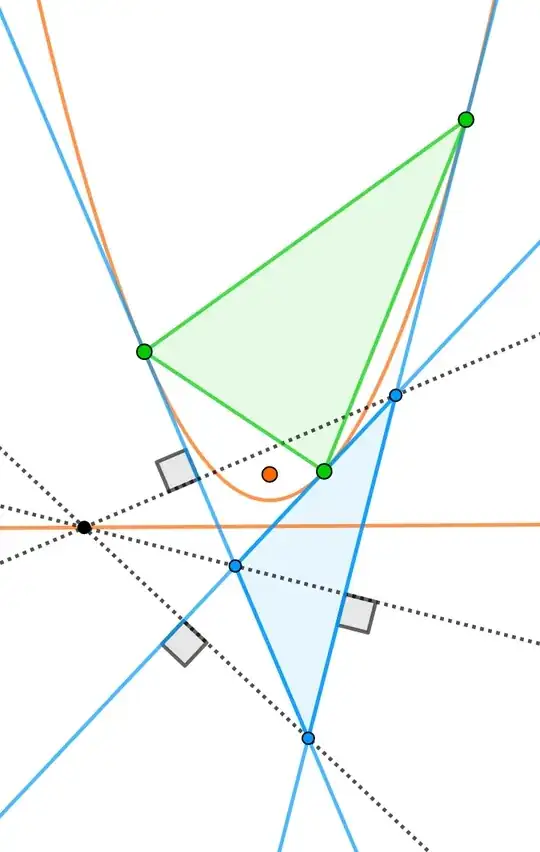If we take three points of a parabola and draw tangents in them, the point of intersection of the altitudes of the triangle of tangents will lie on the directrix of the parabola.

It's clear how to prove this with analytic geometry by mapping the equations of these altitudes and assigning the coordinates of the point of intersection of two of them, but I wonder if there is a geometric approach to prove this

If there is any reference that talks about the property, please mention it, thank you

Edit: Another feature I just came up with relates to the same format and it's so easy I don't need help with it but I'll just mention it to link the relevant information to each other: 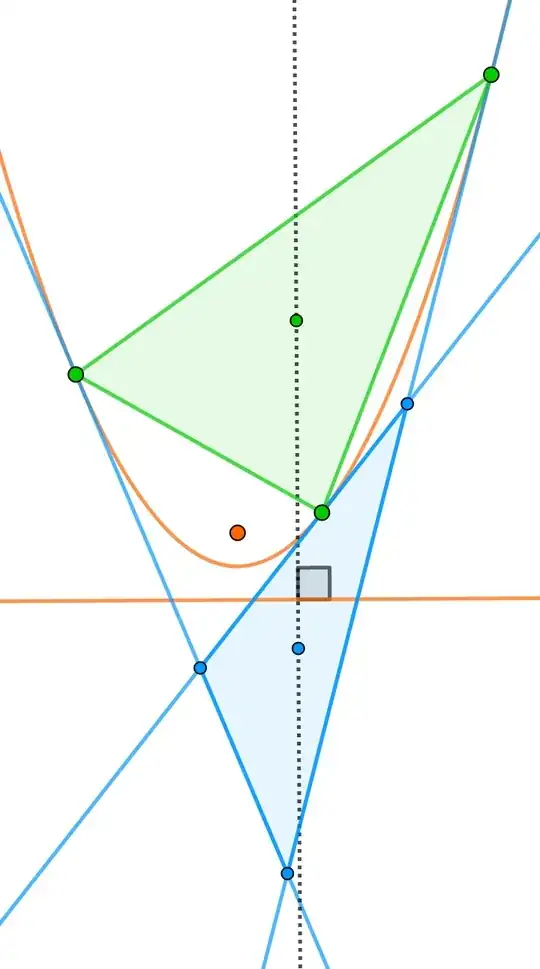the straight line connecting the center of gravity of the parabola triangle to the center of gravity of the triangle of tangents must be perpendicular to the directrix.

I used a compiler keyboard to write that, so the writing may not be accurate, please do not hesitate to correct me when you notice any error, I think the data and what is required are clear from the image @Gwen — زكريا حسناوي, Apr 26 '24 at 03:22
FYI: The first property matches the first part of this question "Prove: Three tangents to a parabola form a triangle with an orthocenter on the directrix and a circumcircle passing through the focus", which appears to be a textbook exercise, so the property is evidently known. (Note that this does not diminish your accomplishment in re-discovering it. Congratulations!) — Blue, Apr 26 '24 at 03:57
A very interesting question - I think I saw a similar diagram in an old textbook recently, so I'm currently hunting through files to see if there is a name for this theorem. If I find one I will post an answer (unless beaten to it, of course). — Red Five, Apr 26 '24 at 04:15
Thank you @blue , I knew the property that the circle around the triangle of tangents passes through the focal point of the parabola but I didn't know that the point of convergence of heights belongs to the parabola index until today, and now I have shown that this is also known, I will try to look for more new theorems — زكريا حسناوي, Apr 26 '24 at 04:16

score 1 · Accepted Answer · answered Apr 26 '24 at 05:09

1

Since you asked for a geometric proof, see Russell, Pure Geometry, Ex 8, pg 161. It is a clever application of Brianchon's Theorem, where two vertices of the Brianchon hexagon are points at infinity.

answered Apr 26 '24 at 05:09

brainjam

9,172

Thank you @brainjam – زكريا حسناوي Apr 26 '24 at 05:23

score 1 · Answer 2 · answered Apr 26 '24 at 14:49

1

This is proof of the second theorem in Arabic:

answered Apr 26 '24 at 14:49

زكريا حسناوي

4,060
7
25

score 1 · Answer 3 · answered Jun 12 '24 at 00:37

Here's another beautiful geometric proof from Smith, Geometrical Conics, 1894, pg 239, Article 181.

The first sentence ("we know that all conics .." etc.) refers to Prop. XXIX on pg 165:

The remainder of the proof ("Reciprocating with respect to the orthocentre .." etc) refers to the concept of reciprocation, which is explained starting on page 234.

Given a parabola, does the orthocenter of a triangle of tangents lie on the directrix?

3 Answers3