Conjecture: Generalization of the triangle inequality to exponents of the sides

Question

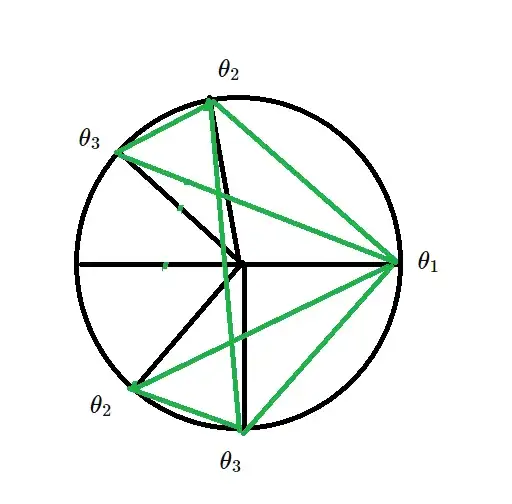
Let $(x,y,z)$ be the sides of a triangle whose vertices are uniformly random on the circumference of a circle. Experimental data using a simulation with $10^9$ trails for each tested value of $a \ge 1$ suggests that:

When $a \ge 1$ then the probability that $x^a + y^a \ge z^a$ is $P\left(x^a + y^a \ge z^a\right) = \frac{2}{3} + \frac{1}{3a^2}$, or equivalently if $x \le y \le z$. Then $P\left(x^a + y^a \ge z^a\right) = \frac{1}{a^2}$.

Can this Conjecture be proved or disproved? Related question.

Julia source code

using Random
step = 10^9
while true
    a = 1
    while true
        f = 0
        for _ in 1:step
            angles = rand(3) .* 6.283185307179586
            vertices_x = cos.(angles)
            vertices_y = sin.(angles)
            push!(vertices_x, vertices_x[1])
            push!(vertices_y, vertices_y[1])
        x_diff = diff(vertices_x)
        y_diff = diff(vertices_y)
        side_lengths = sqrt.(x_diff.^2 .+ y_diff.^2)
        x, y, z = side_lengths

        if x^a +y^a >= z^a
            f += 1
        end
    end
    prob = f/step
    println((a, prob, prob / (2/3*(1 + 1/2/a^2))))

    a = round(a + 0.1, digits=10)
end

end

Answer 1

The conjecture is proved at MathOverflow Question No. 469729.

Answer 2

Proof for $a=2$ can be somewhat easy.

We get $P=3/4$ when $a=2$
It is related to Pythagorean Theorem $x^2+y^2=z^2$ occurring when middle angle $\theta_2$ is $90^\circ$.
Hence , when first angle $\theta_1$ is arbitrarily selected & rotated to $0^\circ$ , then second angle $\theta_2$ & third angle $\theta_3$ can be on the two semicircles formed by the Diameter through the first angle $\theta_1$.

Pictorially :

We can see various $\theta$ angles.
Both on upper semicircle will give obtuse angle & inequality will not hold.
One on upper semicircle & One on lower semicircle will give acute angle & inequality will hold.
Both on lower semicircle will give acute angle & inequality will hold.
Calculating Probability , we have to check the good Pair versus bad Pair , when $\theta_2$ is between $0$ & $2\pi$ , while $\theta_3$ is between $\theta_2$ & $2\pi$
It is like this :

Bad Pair (Blue Area) is $1/4$ while good Pair (Purple Area) is $3/4$.

Process is same for other $a$ values , though visualization & integration might be cumbersome.

Answer 3

Long comment: geometric interpretation

---

Suppose a triangle has side lengths $a,b,c$ where $c$ is the longest.

In the diagram, the triangle shares a base of length $c$ with the orange region. The orange region is bounded above by circular arcs of radius $c$, centred at the triangle's bottom vertices. The triangle's top vertex must lie within the orange region, because $c$ is the longest side length.

Now let's see what triangles look like when they satisfy $a^p+b^p>c^p$.

Suppose the top vertex has coordinates $(x,y)$. Pythagorus gives $a=\sqrt{x^2+y^2}$ and $b=\sqrt{(c-x)^2+y^2}$.

If $a^p+b^p=c^p$ then $(x^2+y^2)^\frac{p}{2}+((c-x)^2+y^2)^\frac{p}{2}=c^p$. This is the equation of the green curve.

If $a^p+b^p>c^p$ then the top vertex must lie above the green curve, but still in the orange region. So we can see what triangles look like when they satisfy $a^p+b^p>c^p$.

It can be shown that, as $p$ increases, the green curve approaches the upper boundary of the orange region. (A general point on the left boundary of the orange region has coordinates $(x, c+\sqrt{c^2-y^2})$; plug this into the LHS of the equation of the green curve, and you will see that it is approximately equal to the RHS of the equation of the green curve, when $p$ is large. Same for the right boundary.) This gives an intuition why, if the triangle is a randomly inscribed triangle in a circle, then $P(a^p+b^p>c^p)\to 0$ as $p\to\infty$.