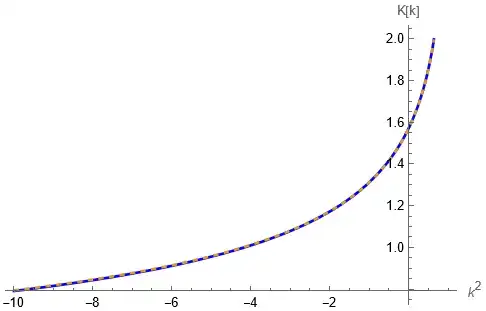
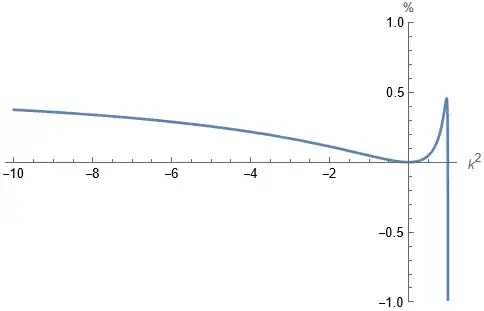
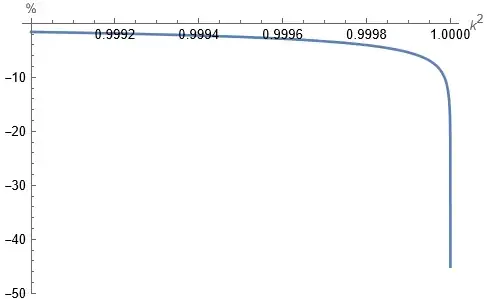
Finding an approximation for the complete elliptic integral of the first kind $K(k)$

Question

Finding an approximation for the complete elliptic integral of the first kind $K(k)$

In this question the author find the following approximation to the integral: $$ I(k) := \int\limits_{0}^{\frac{\pi}{2}} \sqrt{\sin^2(a)+k^2\cos^2(a)}\,da \approx \dfrac{\pi k}{\left(|k|+1\right)\sin\left(\frac{\pi k}{|k|+1}\right)}:= g(k) \label{Eq. 1}\tag{Eq. 1}$$ which works pretty good as you could see in Desmos.

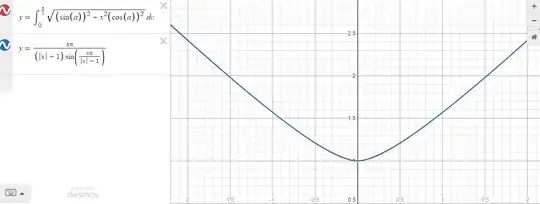
In the same question, in the following answer it is stated that the integral $I(k)$ is related to the complete elliptic integral of the second kind $E(k)$ as: $$I(k) = \sqrt{k^2}E\left(\sqrt{1-\frac{1}{k^2}}\right)$$

and since the complete integral of the first kind $K(k)$ is related to the second kind ones $E(k)$ as: $$E(k) = \left(1+\sqrt{1-k^2}\right)\cdot E\left(\dfrac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}}\right)-\sqrt{1-k^2}\cdot K(k)$$

I want to find an approximation of $K(k)$ in terms of $g(k)$ but I got stack on the modulus transformations, but in principle it looks it is possible to isolate $K(k)$ in terms of $E(k)$ such the approximation $g(k)$ could be introduced:

Could you find an approximation for $K(k)$ in terms of the approximation $g(k)$??

---

Motivation__________

In this another question I was trying to find some formula for the logarithm of large numbers, and in this answer is shown the following approximation: $$\ln(x)\approx\frac{\pi}{2M\big(1,2^{2-m}/x\big)}-m\ln(2)$$ where $M(x,y)$ is arithmetic-geometric mean, and in Wikipedia is stated that this mean is related to the complete elliptic integral of the first kind as: $$M(x,y) = \frac{\pi}{4}\cdot \dfrac{x+y}{K\left(\frac{x-y}{x+y}\right)}$$

and I aim to figure out if a good approximation could be built using $g(k)$.

Answer 1

The initial expression can be rewritten using $\theta=\pi/2-a$, as: $$ I(k) = \int_\limits{0}^{\pi/2}\hspace{-1ex} da\ \sqrt{\sin^2 a +k^2\cos^2 a} = \int_\limits{0}^{\pi/2}\hspace{-1ex} da\ \sqrt{1 - (1-k^2)\cos^2a} \\ = \int_\limits{0}^{\pi/2}\hspace{-1ex} d\theta\ \sqrt{1 - (1-k^2)\sin^2\theta} = E(\sqrt{1-k^2}), \tag{1} $$ where the last step is just using the definition of Wikipedia. This is of course the same as the expression you obtained from this answer, so that just proves that $k\ E\big(\sqrt{1-\frac1{k^2}}\big) = E(\sqrt{1-k^2})$.

Renaming $k$ as $q$, from $(1)$ we get $E(\sqrt{1-q^2}) = I(q)$ and we can derive: $$\begin{align} E(k) &= I\big(\sqrt{1-k^2}\big), \quad\text{by solving}\ \ k=\sqrt{1-q^2} \ \ \text{for}\ \ q, \ \ \text{and} \\[5pt] E\Big(\frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}}\Big) &= I\Big(\frac{2(1 - k^2)^{1/4}}{1 + \sqrt{1 - k^2}}\Big) \quad\text{by solving}\ \ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} =\sqrt{1-q^2} \end{align}$$ We then have the two values of $E$ that we need to use the relation: $$E(k) = \big(1+\sqrt{1-k^2}\big) E\left(\dfrac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}}\right)-\sqrt{1-k^2}\ K(k),$$ which then leads to: $$K(k) = -\frac{I\big(\sqrt{1-k^2}\big)}{\sqrt{1-k^2}} +\frac{\big(1+\sqrt{1-k^2}\big)}{\sqrt{1 - k^2}}\ I\Big(\frac{2(1 - k^2)^{1/4}}{1 + \sqrt{1 - k^2}}\Big)$$ And of course we can now try to use the approximation by $g$ for both occurrences of $I$, which would give us: $$K(k) \approx -\frac{g\big(\sqrt{1-k^2}\big)}{\sqrt{1-k^2}} +\frac{\big(1+\sqrt{1-k^2}\big)}{\sqrt{1 - k^2}}\ g\Big(\frac{2(1 - k^2)^{1/4}}{1 + \sqrt{1 - k^2}}\Big).$$ Since this is clearly a function of $k^2$, we can plot it for negative $k^2$ as well. Here's a plot from $k^2=-10$ to $1$:

Fig.1. $K(k)$ versus $k^2$ (blue) and the approximation (red).

Fig.2. The relative error in the approximation (percentage).

As can be seen the error is less than 0.5% over most of the range, but when we approach the singularity at $k=1$, we get an error of up to 50%:

Fig.3. Relative error in the approximation (percentage) for $k\rightarrow 1$.

Answer 2

Assuming $k>0$ and $$g= \dfrac{\pi k}{\left(k+1\right)\sin\left(\frac{\pi k}{k+1}\right)}$$ we could try to compute the inverse $$x=\frac{\pi k}{k+1}\qquad \implies \qquad \frac 1 g=\frac{\sin (x)}{x}$$

You can have a good approximation of $\frac{\sin (x)}{x}$ using the $[2n,2n]$ Padé approximants $P_n$ such as $$P_1=\frac {1-\frac{7}{60}x^2} {1+\frac{1 }{20}x^2}\qquad \text{or}\qquad P_2=\frac {1-\frac{53 }{396}x^2+\frac{551 }{166320} x^4} {1+\frac{13 }{396}x^2+\frac{5 }{11088}x^4}$$ whose errors are respectively $\frac{11 x^6}{50400}$ and $\frac{11 x^{10}}{457228800}$.

To give an idea of the accuracy $$\Phi_n=\int_0^\pi \Bigg(\frac{\sin (x)}{x}-P_n \Bigg)^2\, dx$$ they are respectively $\Phi_1=3.01\times 10^{-3} $ and $\Phi_2=2.78\times 10^{-7}$.

If you prefer series expansion followed by series reversion

$$x=t+\frac{t^3}{40}+\frac{107 t^5}{67200}+O\left(t^7\right)\qquad \text{wher}\qquad t=\sqrt{\frac{6(g-1)}{g}}$$

So, you have $k(g)$.