Isomorphism between deck transformations and permutations onto the fiber

Question

I came across this problem in Fulton's Algebraic topology textbook (problem 11.39) and I can't seem to get to the bottom of it. The problem is as follows:

Let $p:Y\to X$ be a covering, with $Y$ connected and $X$ path-connected. Let $x\in X$, and set $S=p^{-1}(x)$. Any automorphism of the covering restricts to a permutation of $S$, and the automorphism is determined by this restriction, so Aut$(Y/X)\subset$ Aut$(S)$. Show that Aut$(Y/X)\simeq \{\varphi\in\text{Aut}(S): \varphi(z*\sigma)=\varphi(z)*\sigma\;$ for all $z\in S$ and all closed paths $\sigma$ at $x\}$

To be clear with the notation, Fulton defines $y*\gamma$ to be the ending point of the lifted path $\tilde{\gamma}$ with starting point at $y$ ($y*\gamma=\tilde{\gamma}_y(1)$)

I managed to show that Aut$(Y/X)\subset$ Aut$(S)$ and one inclusion (Aut$(Y/X)\subseteq \{\varphi\in\text{Aut}(S): [...]\}$) but I'm not being able to show the other inclusion. Does anyone have a clue on how to approach the problem?

Answer 1

Fix $y\in p^{-1}(x)$. If $Z$ is path connected and locally path connected, $f\colon Z\to X$ a map and $z\in Z$ such that $f(z) = x$, then there is a lift $F\colon Z\to Y$ of $f$ with $F(z)=y$ iff $f_\ast(\pi_1(Z,z))\subset p_\ast(\pi_1(Y,y))$. If one of these conditions is true, $F(z')$ is defined as follows. Take any path $\alpha$ from $z$ to $z'$ and lift the path $f\circ \alpha$ in $X$ to the path $\beta$ in $Y$ starting at $y$ and put $F(z')=\beta(1)$.

In the case at hand let $y\in S=p^{-1}(x)$ and suppose $\varphi\in \mathrm{Aut}(S)$ satisfies the condition of the question. If we know that $p_\ast(\pi_1(Y,y)) = p_\ast(\pi_1(Y,\varphi(y))$ we get a map $f\colon Y\to Y$ that lifts $p\colon Y\to X$ with the property that $f(y)=\varphi(y)$, that is it is an automorphism of coverings. I leave it to you to check that in this case the restriction of $f$ to $S$ is equal to $\varphi$.

To see that $p_\ast(\pi_1(Y,y)) = p_\ast(\pi_1(Y,\varphi(y))$, let $\alpha\in \pi_1(Y,y)$ and $\beta$ a lift of $p_\ast(\alpha)$ starting at $\varphi(y)$. Then by definition $$\beta(1) = \varphi(y)\ast p_\ast(\alpha) = \varphi(y\ast p_\ast(\alpha)) = \varphi(\alpha(1)) = \varphi(y),$$ which means that $\beta\in \pi_1(Y,\varphi(y))$ and by assumption $p_\ast(\beta) = p_\ast(\alpha)$, hence $p_\ast(\pi_1(Y,y)) \subset p_\ast(\pi_1(Y,\varphi(y))$ and the reverse inclusion is completely analogous.

Answer 2

I am not surprised that you were not able to show the other inclusion. Under the given conditons "$Y$ connected and $X$ path-connected" it is in general not true. See Vincent Boelens's answer for a proof under stronger assumptions.

Here is a counterexample. Let $T \subset \mathbb R^2$ denote the closed topologist's sine curve $T = L \cup S$ with $L = \{0\} \times [-1,1]$ and $S= \{\left(x, \sin(\frac \pi x)\right) \mid x \in (0,1] \}$. Let $\tau_n : \mathbb R^2 \to \mathbb R^2$ denote the translation by the vector $(0,n)$ with $n \in \mathbb Z$. Define $T_n = \tau_n(T)$. We have $T_n \cap T_{n+1} = \{(n+1,0)\}$ and $T_n \cap T_m =\emptyset$ if $m \ge n+2$. Now define $$Y = \bigcup_{n \in \mathbb Z} T_n .$$

$Y$ is an infinite chain of copies of $T$. It is well known that $T$ is connected and has two path-components ($L$ and $S$) which are contractible. Hence $Y$ is connected and has infinitely many path components $P_n = \tau_n(S) \cup \{n+1\} \times [-1,1]$ which are contractible.

The additive group $\mathbb Z$ operates on $Y$ via the translations $\tau_n$ (which restrict to homeomorphisms on $Y$).

The quotient $X = Y /\mathbb Z$ of this operation is nothing else than the quotient space $T/E$ obtained by identifying $E= \{ (0,0), (0,1)\}$ to a single point. The quotient map $p : Y \to X$ is a covering map. This is completely analogous to the standard covering map $p : \mathbb R \to [0,1]/\{0,1\} = S^1$.

The space $X = T/E$ is a variant of the Warsaw circle:

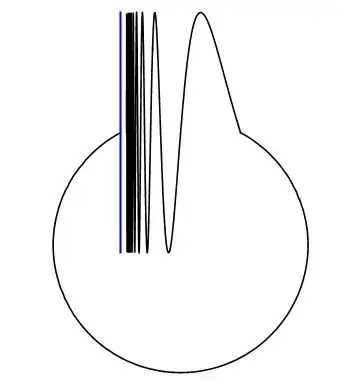
It is well-known that this space is path-connected and simply connected (it has no non-contractible loops).

Pick any $x \in X$. Then $S =p^{-1}(x)$ is countably infinite. Since $X$ is simply connected, lifts of closed paths are again closed paths. Thus $z * \sigma = z$ for all $z \in S$ so that the condition $\varphi(z*\sigma)=\varphi(z)*\sigma$ is satisfied for all $\varphi \in \operatorname{Aut}(S)$.

However, the only deck transformtions of $Y$ are the translations $\tau_n$. This shows that $\operatorname{Aut}(Y/X) \subsetneqq \operatorname{Aut}(S)$.