This question was asked in one of sample paper. So I don't have an answer for this. It is as follows
Two friends A, B are planning to meet at the bus stop between 2 and 3 pm. The agreement between them is that after one arrives they will wait till other shows up, 15 minutes passed or it becomes 3 pm, whichever is earlier. Probability that they will both meet is ? (It had four options, A) 1/4 B) 3/16 C) 13/16 D) 3/4)
MY APPROACH
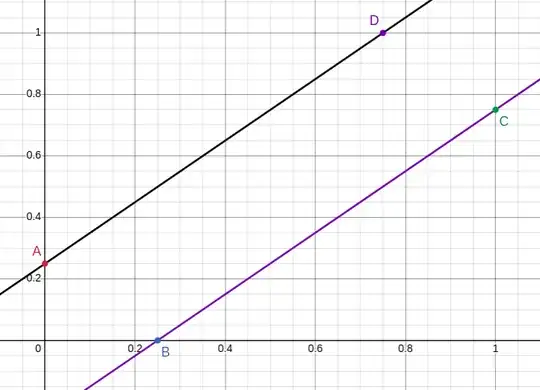
Let X, Y be the arrival times and we can assume that they are distributed as $U(0, 1)$ and are independent. So for them to meet we should have $|X - Y| < 1/4$.
As per the diagram the region of interest will be between the two lines. The lines are $x - y = \frac{1}{4}$ and $ y - x = \frac{1}{4}$. The area of triangle will be $ \frac{1}{2} \times \frac{3}{4} \times \frac{3}{4} = \frac{9}{32}$. So the area of region will be $1 - 2 \times \frac{9}{32} = \frac{7}{16}$ which is not present in any of the option. So wanted to know if I am doing something wrong or was the options wrong ?