The primorial numeral system is a numeral system whose interest I am trying to establish mathematically.
Unfortunately, my mathematical knowledge is limited, so I would like to briefly present some results in the hope that you will correct any mathematical inaccuracies.
$2,3,5$ are the first three primes. $2\times 3\times 5=30$ is called the third primorial. On $\mathbb Z/30\mathbb Z$, we have the classical structure of ring. We also have a $\mathbb Z$-module structure $(\mathbb Z/30\mathbb Z,+,.)$, where for example by writing $\bar 8$ the class of integers $\bar 8=8+30\mathbb Z, $ we have $$3.\bar 8:=\bar 8+\bar 8+\bar 8$$By Chinese Remainder Theorem, we also have $$\mathbb Z/30\mathbb Z\approx \mathbb Z/2\mathbb Z \times \mathbb Z/3\mathbb Z\times\mathbb Z/5\mathbb Z $$and $\mathbb Z/2\mathbb Z \times \mathbb Z/3\mathbb Z\times\mathbb Z/5\mathbb Z =\mathbb Z/2\mathbb Z \times \mathbb Z/3\mathbb Z\times \{0\}+\{0\}\times\{0\}\times \mathbb Z/5\mathbb Z=\color{blue}{5\mathbb Z/30\mathbb Z }+\color{darkgreen}{6\mathbb Z/30\mathbb Z} $
For example, $$\overline {17}=5.\bar 1+6.\bar 2$$
This whole long preamble will be amply illuminated, I hope, by the following drawing, illustrating the modular structure
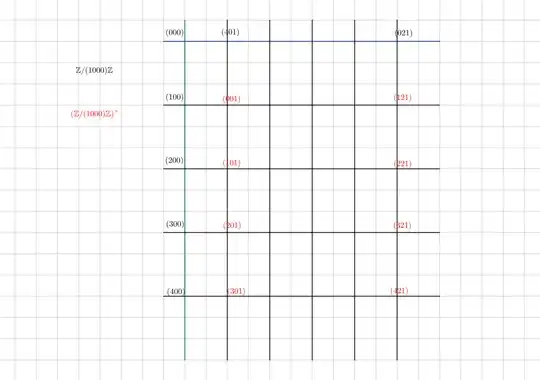Questions
1.- Does this work on a mathematical object as well-known as $Z/30Z$ seem mathematically correct to you?
2.- Does it at least correspond to the beginning of the foundation of the mathematical interest of primorial numeration? (I would like to point out that on the illustration provided, one can very easily highlight the object $J$ which seemed to arouse interest among some members of MSE but for which I did not obtain any reference)
Note :
- Let $u\in \mathbb Z/30\mathbb Z$ such that $\exists v\in \mathbb Z/30\mathbb Z, uv=1$. $u$ is called a unit of $\mathbb Z/30\mathbb Z$. By application of Bézout's theorem, the units of $\mathbb Z/30\mathbb Z$ contains all primes except $2,3$ and $5$.
- Group of units of $\mathbb Z/30\mathbb Z$ is denoted by $$(\mathbb Z/30\mathbb Z)^\times=\{-13,-11,-7,-1,1,7,11,13\}$$
- In Primorial numeral system $$(a:b:c)_{primorial}\overset{\text{def}}{=}a\times 6+b\times 2+c$$ Example : $(2:2:1)_{primorial}\overset{\text{def}}{=}2\times 6+2\times 2+1$
- Primorials are defined by induction :
Let $p_1=2, p_2=3, p_3=5,p_4=7,p_5=11,...$ the primes
We define $p_1\#=p_1=2, p_2\#=p1\times p_2=2\times 3=6$ and for $n\geq 1$ $$p_{n+1\#}:=p_{n+1}\times p_{n\#}$$
$$\boxed{(p_n\#)_{n\geq 1}=(2;6;30;210;2\,310;30\,030;...)}$$
