Questions about $\mathbb Z/30\mathbb Z$

Question

I'm interested in the ring $(\mathbb Z/30\mathbb Z,+,\times)$, the elements of which I'll write down in bold. For example $$\textbf{7}=7+30\mathbb Z=\{...-83,-53,-23,7,37,67...\}.$$ I'm interested in particular with $$U:=(\mathbb Z/30\mathbb Z)^\times=\{\textbf{1},\textbf{7},\textbf{11},\textbf{13},\textbf{17},\textbf{19},\textbf{23},\textbf{-1}\}$$ because every prime except $2,3$ and $5$ does belong to one of theses classes of numbers. 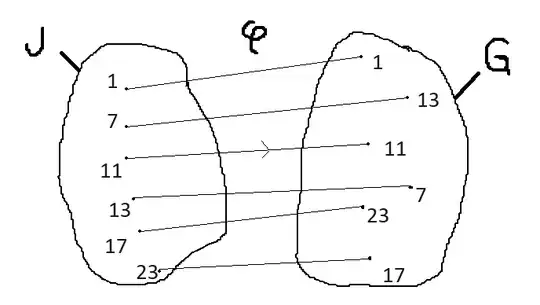There is a lot of things to say about $\mathbb Z/30\mathbb Z$, but those are the types of objects that interest me : $$\boxed{J\overset{def1}=\{p\in (\mathbb Z/30\mathbb Z)^\times|p+\textbf{6}\in (\mathbb Z/30\mathbb Z)^\times \}}$$For example, $\textbf{19}\notin J$ $$\boxed{G\overset{def2}=\{p\in (\mathbb Z/30\mathbb Z)^\times|6p+\textbf{1}\in (\mathbb Z/30\mathbb Z)^\times\}}$$About $J$ and $G$, there's a result that I find interesting about involution defined below$$\boxed{\varphi:U\to U, u\mapsto u^{-1}\text{ induces bijection }\varphi_{/J}:J\to G}$$since $u\in J\overset{def1}\iff u+\textbf{6}\in U \iff u^{-1}(u+\textbf{6})\in U\iff \textbf{1}+6u^{-1}\in U\overset{def2}\iff u^{-1}\in G$

---

Edit (to generalize, see question 3):

let $p_1=2,p_2=3,p_3,...$ the prime numbers. $$\forall n \in \mathbb N^*, p_n\#:=p_1...p_n\text{ (n-th primorial)}$$ $$U_n:=(\mathbb Z/p_n\#\mathbb Z)^\times$$ $$J_n:=\{p\in U_n|p+6\in U_n\}$$ $$G_n:=\{p\in U_n|6p+1\in U_n\}$$ $$\text{result :}|J_n|=2(p_n-2)...(p_2-2). \text{So, }\lim_{n \to \infty}|J_n|=+\infty$$

---

My questions:

1.- I was wondering if $J$ and $G$ were given names and if not, why?

2.-If you have other simple results like this in $(\mathbb Z/30\mathbb Z)^\times$, for example like $|J|=|G|=2(5-2)(3-2)=6$, where $|X|$ denotes the number of elements of a set $X$.

3.- These results easily extend to $\mathbb Z/210\mathbb Z(\text{for example }, |J_4|=|G_4|=2(7-2)(5-2)(3-2)), \mathbb Z/2310\mathbb Z, ..., \mathbb Z/p_n \# \mathbb Z$.

Does the switch to $\mathbb Z/210\mathbb Z$ bring any interesting new results?

Answer 1

Since I have not received a reply, I do not think it is inappropriate to propose names to $J$ and $G$( in my answer, I will not use bold notation but the usual misuse of notation.)

To make the name I give them understood, it is necessary to generalize. Let $n,m\in \mathbb N^*$. $$U_n:=(\mathbb Z/p_n\#\mathbb Z)^\times$$ $$J_{n,m}:=\{p\in U_n|p+p_m\#\in U_n\}$$ $$G_{n,m}:=\{p\in U_n|p_m\#.p+1\in U_n\}$$

Examples :

$$p_1\#=2, p_2\#=p_1.p_2=2\times 3=6$$ $$J_{n,1}:=\{\color{red}p\in U_n|\color{red}{p+2}\in U_n\}, G_{n,1}:=\{\color{red}p\in U_n|\color{red}{2p+1}\in U_n\}$$ $$J=J_{3,2}, G=G_{3,2}$$

Defining these objects and studying them is obviously inspired by Sophie Germain's numbers and twins(Jumeaux in French). So I call them "m-order twins in $\mathbb Z/p_n\#\mathbb Z$" and "m-order Germains".

Hence my $J$ and $G$ notations of the original post. I hope that this will be a little clearer, as my questions are still open.

---

Coefficients $$\alpha_m=\frac{|J_{n,m}|}{|J_{n,1}|}$$do not depend on $n$.$$(\alpha_m)_{m\geq 2}=(2,\color{green}{\frac83},\frac{16}{5},...), \alpha_{m}=\alpha_{m-1}\frac{p_m-1}{p_m-2}$$

---

It is clear that the modular objects considered before have little to do with prime numbers. However, let's consider a long list of prime numbers and count $p$ such that $p+30$ is also prime and $p$ such that $p+2$ is also prime. If we calculate the ratio between these two results, we find a number close to $\color{green}{\frac83}$

Answer 2

As you already observed that $J$ and $G$ are in bijection, so let’s just focus on $J$. These results generalize to a wider setting, not necessarily in your formulation of $p_n^{\#},$ i.e. the $n$-th primorial. More precisely, your observations can be derived from the following results, which follow in turn from solving congruences and applying the Chinese Remainder Theorem.

Lemma 1. Let $n=p^m,m\geq 1, p~{\rm a ~prime ~and~}a\in {\mathbb Z}.$ Define $U_n$ and $J_n(a)$ by $$U_n=\left({\mathbb Z}/n{\mathbb Z}\right)^\times~{\rm and~}J_n(a)=\{u\in U_n~|~u+a\in U_n\}.$$ Then $$|J_n(a)|=\left\{\begin{array}{cc}|U_n|=\varphi(p^m)=(p-1)p^{m-1},&~{\rm if~}p \mid a\\ p^m-2p^{m-1}=(p-2)p^{m-1},&~{\rm if~}p\nmid a.\end{array}\right.$$ This motivates the following definition (not sure if this exists in the literature).

Definition 1. For a prime number $p,$ integer $m\geq 1,$ and $a\in {\mathbb Z},$ define $\varphi_a(p^m)$ by $\varphi_a(p^m)=\varphi(p^m)$ if $p\mid a$, and $\varphi_a(p^m)=p^m-2p^{m-1}$ if $p\nmid a.$

Lemma 2. Let $n=p_1^{m_1}\cdots p_r^{m_r},r\geq 2,m_1,\cdots,m_r\geq 1,~{\rm and~}p_1,\cdots,p_r$ be distinct primes. Let $$U_n=\left({\mathbb Z}/n{\mathbb Z}\right)^\times \simeq \prod_{k=1}^r\left({\mathbb Z}/p_k^{m_k}{\mathbb Z}\right)^\times$$ and $$J_n(a)=\{u\in U_n~|~u+a\in U_n\}.$$ Then $$|J_n(a)|=\prod_{k=1}^r|J_{p_k^{m_k}}(a)|=\prod_{k=1}^r\varphi_a(p_k^{m_k}),$$ where $\varphi_a$ is as in Definition 1.

As in the beginning paragraph, the proof is by the Chinese Remainder Theorem. Here one includes two examples.

Example 1. For $n=3^4\cdot 7\cdot 11^2,a=2\cdot 5\cdot 7,$ one has $$|J_n(a)|=(3^4-2\cdot 3^3)(7-1)(11^2-2\cdot 11)=16038.$$

Example 2. For $n=2^3\cdot 5\cdot 7^2\cdot 11,a=2^2\cdot 3\cdot 7,$ one has $$|J_n(a)|=(2^3-2^2)(5-2)(7^2-7)(11-2)=4536.$$

Note. In Question 2, you have $a=6=2\cdot 3, n=30=2\cdot 3\cdot 5,$ so by Lemma 2, $$|J|=(2-1)(3-1)(5-2)=6.$$ Similarly, in Question 3, $a=6=2\cdot 3,n=210=2\cdot 3\cdot 5\cdot 7,$ hence $$|J|=(2-1)(3-1)(5-2)(7-2)=30.$$