How did Artin discover the function $f(x)=\frac{(x^2-x+1)^3}{x^2(x-1)^2}$ with the properties $f(x)=f(1-x)=f(\frac{1}{x})$?

Question

In Artin's "Galois Theory" P38, he said the function $$f(x) = \frac{(x^2 - x + 1)^3}{x^2(x-1)^2}$$ satisfies the properties of $f(x)=f(1-x)=f(\frac{1}{x})$.

Is the function given by some rational step or just by a flash of insight？

If $f(0)$ is a number, then $f(0) = f(\frac{1}{0})$. So that the domain of definition of f(x) does not include 0.(maybe. I know it's not rigorous) Then the domain of definition of f(x) does not include 1 either. Thus I think it is a function like $f(x)=\frac{g(x)}{x^a(x-1)^bh(x)}, h(0)*h(1) \neq 0$. Then I tried $a=1, b=1$, failed. but $a = 2, b = 2$ succeed.

However, I think that's a really weird way to go about it. Does the question like" $f(x)$ is a rational function that satisfies the properties of $f(x) = f(g_1(x)) = f(g_2(x)) = ... =f(g_n(x)). \forall k \in \mathbb N^+, g_k(x)$ is a rational function. Now give a example of f(x)." has an easy way to solve?

Answer 1

Note that $g(x) = 1-x $ and $h(x) = \frac{1}{1-x}$ generate a subgroup $G$ of the Möbius group $\mathrm{Aut}(\hat{\mathbb{C}})$ that is isomorphic to $S_3$ via the relations:

$$ g^{2} = \mathrm{id}, \qquad h^{3} = \mathrm{id}, \qquad ghgh = \mathrm{id} $$

Note that $G$ also contains $h(g(x)) = \frac{1}{x}$ and that $G$ is also generated by $g$ and $hg$, which explains why $G$ is related to OP's question.

Now define $f(x)$ by

$$ f(x) := \sum_{\sigma \in G} \frac{\sigma(x)(\sigma(x) + 1)}{2}. \tag{1} $$

Then clearly $f(\tau(x)) = f(x)$ for any $\tau \in G$. Moreover, it turns out that this $f(x)$ is precisely what OP asked:

$$ f(x) = \frac{(x^2-x+1)^3}{x^2 (x-1)^2}. $$

---

Here is a possible explanation for the choice of $f(x)$. Consider the region

$$ U = \{ z \in \mathbb{C} : |z| < 1 \text{ and } |1-z| < 1 \text{ and } \operatorname{Im}(z) > 0 \}. $$

This $U$ corresponds to reddish region in the figure below:

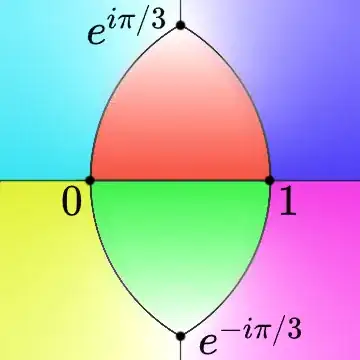
Then $\sigma(\overline{U})$ for $\sigma \in G$ forms a non-overlapping division of the Riemann sphere $\hat{\mathbb{C}}$, each of which corresponding one of the six colored regions in the figure above.

Now, as the figure suggests, the points $e^{\pm i\pi/3}$ play special roles, in that $\sigma(e^{\pm i\pi/3}) = e^{i\pi/3}$ or $e^{-i\pi/3}$ for each $\sigma \in G$. In fact,

• exactly three elements of $G$ maps $e^{i\pi/3}$ to $e^{i\pi/3}$, and
• the remaining three maps $e^{i\pi/3}$ to $e^{-i\pi/3}$.

This tells that

$$ \sum_{\sigma \in G} \sigma(e^{i\pi/3})^2 = 3(e^{i\pi/3} + e^{-i\pi/3}) = -3. $$

This and the identity

$$ \sum_{\sigma \in G} \sigma(x) = \frac{1}{2} \left[ \sum_{\sigma \in G} \sigma(x) + \sum_{\sigma \in G} g(\sigma(x)) \right] = 3 $$

together, we know that $f(x)$ has the factor $x^2 - x + 1$. Moreover, since the figure above tells that three regions meet at each of $e^{\pm i\pi/3}$, it is not unreasonable to expect that $f(x)$ contains multiple copies of $x^2 - x + 1$.

Although I don't have enough expertise to pursue this direction, I believe Artin had certain understanding on this kind of topic when he designed the function $f(x)$.

Answer 2

Let $K = \mathbf C(x)$. This is a field with automorphisms $r$ and $s$ where $r(h(x)) = h(1/(1-x))$ and $s(h(x)) = h(1/x)$: In other words, $r$ and $s$ are linear-fractional changes of variables $x \mapsto 1/(1-x)$ and $s \mapsto 1/x$. Check $r$ has order $3$, $s$ has order $2$, and $r(s(h)) = s(r^2(h))$ for all $h \in K$. So $\langle r,s\rangle \cong S_3$.

Since $r(s(h)) = r(h(1/x)) = h(1/(1/(1-x))) = h(1-x)$, the way you describe your problem puts emphasis on $r$ and $rs$, which both have order $2$, but they generate the same group as $r$ and $s$: $\langle r,s\rangle = \langle rs,s\rangle$.

If a finite group $G$ acts as automorphisms on a field $K$, then $K^G := \{\alpha \in K : g(\alpha) = \alpha {\rm \ for \ all \ } g \in G\}$ is the subfield of $K$ consisting of elements in $K$ fixed by all of $G$ and Artin proves in the book that $K$ is a Galois extension of $K^G$ with ${\rm Gal}(K/K^G) \cong G$. When $\alpha \in K$, the polynomial $\prod_{g \in G} (T - g(\alpha))$ has coefficients all fixed by $G$: they're in $K^G$.

The simplest coefficients in that polynomial are its 2nd leading coefficient $-\sum_{g\in G} g(\alpha)$ and its constant term $\pm\prod_{g \in G} g(\alpha)$. These are the trace and norm maps from $K$ to $K^G$ on $\alpha$, up to sign: $$ {\rm Tr}(\alpha) = \sum_{g \in G} g(\alpha), \ \ \ {\rm N}(\alpha) = \prod_{g\in G} g(\alpha). $$ The values are always in $K^G$.

Applying this to the 1st paragraph, with $G = \langle r,s\rangle$ acting on $K = \mathbf C(x)$, we have ${\rm Tr}(x) = 3$ and ${\rm N}(x) = 1$, which is boring, while $$ {\rm Tr}(x^2) = \frac{2x^6-6x^5+9x^4-8x^3+9x^2-6x+2}{x^2(x-1)^2} $$ and ${\rm N}(x^2) = 1$. That numerator in the trace is irreducible. But $$ {\rm Tr}(x+x^2) = \frac{2x^6-6x^5+12x^4-14x^3+12x^2-6x+2}{x^2(x-1)^2}, $$ which is $$ 2\frac{x^6-3x^5+6x^4-7x^3+6x^2-3x+1}{x^2(x-1)^2} = \frac{2(x^2-x+1)^3}{x^2(x-1)^2}, $$ and that leads to ${\rm Tr}((x+x^2)/2)$ being the rational function you asked about.

Answer 3

The rational complex functions can be transformed by the group of linear fractional Moebius transformations $$w =\frac{\alpha z + \beta}{\gamma z + \delta}$$ given $$\det\left( \begin {array} {cc} a & b \\ c & d \\\end{array} \right) \ne 0.$$ Nesting two Moebius transformations

$$w =\frac{\alpha z + \beta}{\gamma z + \delta}, \ v=\frac{\epsilon w + \zeta}{\eta w + \theta}$$ the coefficient matrix is a product of the matrices, and with det =1, it is a group $SU(2,\mathbb C)$.

In order to work within the complex integers for solutions of algebraic equations with rational coefficients, the subgroup $SU(2,\mathbb Z)$ generated by integer tranlsations $$ z\to z+1, \ z\to z+i$$ and the inversion at the unit circle $$ z\to \frac{1}{z}$$ is the main tool to reduce and produce the representations of the root algebra.