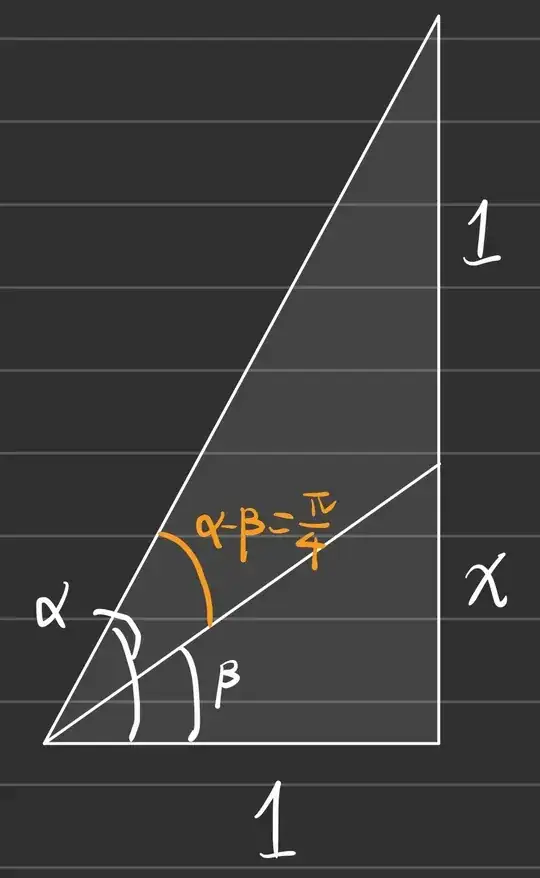
Solve the equation $\arcsin\bigg(\dfrac{x+1}{\sqrt{x^2+2x+2}}\bigg)-\arcsin\bigg(\dfrac{x}{\sqrt{x^2+1}}\bigg)=\dfrac{\pi}{4}$

Question

Solve the equation $$\arcsin\bigg(\dfrac{x+1}{\sqrt{x^2+2x+2}}\bigg)-\arcsin\bigg(\dfrac{x}{\sqrt{x^2+1}}\bigg)=\dfrac{\pi}{4}$$

My solution: I converted this equation in terms of $\arctan$ and applied tangent to both sides, and I got my answer as $x=-1,0$.

But then one of my friends said that $x=2$ satisfies too the above equation, and the reason he gave is as follows: $$\arcsin\bigg(\dfrac{3}{\sqrt{10}}\bigg)=\dfrac{\pi}{4}+\arcsin\bigg(\dfrac{2}{\sqrt{5}}\bigg)$$ and he applied sinus to both sides to obtain $\dfrac{3}{\sqrt{10}}=\dfrac{3}{\sqrt{10}}\:$.

Now I don't have any explanation for him. Can anyone here explain the reason behind this situation?

I plotted it in desmos, and I am getting $x=-1,0$ only.
Link to desmos

Answer 1

COMMENT.-Note that one of the two terms is equal to $0$ when $x=0$ and when $x=-1$. If the other term fits, then you do have solved directly the question. In fact this gives $$\arcsin\left(\frac{1}{\sqrt2}\right)-\arcsin(0)=\frac{\pi}{4}\\\arcsin(0)-\arcsin\left(-\frac{1}{\sqrt2}\right)=\frac{\pi}{4}$$ which is obviously true.

Answer 2

The solution you have obtained is correct and complete. And fully backed by the desmos plot.

Your friend's objection contains a wrong calculation, since we have non-equality $$1.249 \:\approx\:\arcsin\bigg(\frac3{\sqrt{10}}\bigg) \;\neq\; \frac\pi 4+\arcsin\bigg(\frac 2{\sqrt{5}}\bigg) \:\approx\: 1.893\,,$$ see also Blue's comment. Thus, $\,x\!=\!2\,$ does not satisfy the given equation.

---

The given equation can be rewritten as $$\arctan(\,x+1\,)\:=\:\arctan x+\frac\pi 4\,,\tag{1}$$ using the trigonometric identity $\,\sin q =\dfrac{\tan q}{\sqrt{(\tan q)^2 + 1}}$ $\quad\stackrel{\tan q\,=\,x}{\iff}\quad$ $ \arctan x =\arcsin\bigg(\dfrac{x}{\sqrt{x^2 + 1}}\bigg)\,$.

Equation $(1)$ may be solved quickly by applying "$\tan$" and using the angle sum identity: $$\begin{align}x+1 & \:=\:\tan\Big(\arctan x+\frac{\pi}4\,\Big) \:=\: \frac{x+1}{1-x} \\[1.ex] \iff\;(x+1)\cdot x & \:=\: 0 \end{align}$$ Please note $\,1\!-\!x >0\:$ in the denominator because $\,\arctan x=\arctan (x+1)-\frac{\pi}4 <\frac{\pi}2-\frac{\pi}4=\frac{\pi}4\,$.

Answer 3

The reason behind this situation is that $\sin(\pi/2 - \theta) = \sin(\pi/2 + \theta)$, even though $\pi/2 - \theta \neq \pi/2 + \theta$. Given this, $$\sin(\arcsin(\frac{3}{\sqrt{10}})) = \sin(\frac{\pi}{4} + \arcsin(\frac{2}{\sqrt{5}})),$$

but

$$\arcsin(\frac{3}{\sqrt{10}})\neq \frac{\pi}{4} + \arcsin(\frac{2}{\sqrt{5}})$$

The right-hand side is greater than $\pi/2$ and the left-hand side is less than $\pi/2$.

Answer 4

Here is the geometric approach, which can same conclude as other answers. ;)

From the picture above:

$\sin\alpha = \dfrac{x+1}{\sqrt{x^2+2x+2}}, \sin\beta = \dfrac{x}{\sqrt{x^2+1}}$

Therefore, we can say that $\alpha-\beta=\dfrac{\pi}{4}$.

Using the Law of Cosine, $1=x^2+2x+2+x^2+1-\sqrt{2}\sqrt{(x^2+1)(x^2+2x+2)}$.

Solving this, $2x^2+2x+2=\sqrt{2(x^2+1)(x^2+2x+2)}$.

$\Rightarrow \; 2(x^4+2x^3+3x^2+2x+1)=(x^4+2x^3+3x^2+2x+2), $

$x^4+2x^3+3x^2+2x=0, x(x+1)(x^2+x+2)=0.$

Since $x$ is a real number, $x=0$ or $x=-1$ is the only solution.

(Negative $x$ can be understood as the opposite direction!)

Answer 5

Here's an alternative way to confirm $\frac3{\sqrt{10}}$ is not a solution. Apply an identity:

$$\arcsin \frac{x+1}{\sqrt{(x+1)^2+1}} - \arcsin \frac x{\sqrt{x^2+1}} = \arcsin \frac1{\sqrt{x^2+1} \sqrt{(x+1)^2+1}} = \frac\pi4 \\ \stackrel{\sin\square}\implies \sqrt{x^2+1} \sqrt{(x+1)^2+1} = \sqrt2 \\ \stackrel{\square^2}\implies (x^2+1) (x^2+2x+2) = 2 \\ \implies 3x^4 + 3x^2 + 2x = x(x+1)(x^2+x+2)=0$$

The quadratic factor has no real solution, leaving us $x\in\{-1,0\}$.